|
Читайте также: |
Пусть z=f(x,y). Если х и у – функции некоторой переменной t, т.е. x=φ(t), y=ψ(t) то z также является функцией от t. Предположим, что z,x и y имеют непрерывные частные производные по всем своим аргументам. Найдем производную dz/dt.
Дадим аргументу t приращение ∆t, тогда х и y получат приращения ∆x и ∆y, а это значит, что z получит приращение ∆z.
, где ρ - бесконечно малая величина по сравнению с ∆t, т.е. 
.
Разделим все члены равенства на ∆t: 
Пусть ∆t ⇾ 0, тогда ∆x ⇾ 0 и ∆y ⇾ 0, а значит ε ⇾ 0. Переходя к пределу при ∆t ⇾ 0, получим
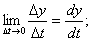
Следовательно: 
(8)
Рассмотрим случай, когда z=f(x,y), а x=φ(u,v), y=ψ(u,v). Тогда z будет функцией от u и v. Предполагая существование непрерывных 
вычислим 
Дадим аргументу u приращение ∆u, сохраняя неизменным значение v. Тогда задача сводится к уже рассмотренному случаю. Значит, dz/dy существует и согласно (8),
(9). Аналогично, 
(10)
Дата добавления: 2015-08-20; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков | | | Неявные функции и их дифференцирование. |