Неявные функции и их дифференцирование.

Неявная функция. Уравнение F(x,y,z)=0 в окрестностях точек (x₀,y₀,z₀), для которых уравнение имеет хотя бы один корень z₀, задает неявную функцию z=f(x,y), значения которой равны корням этого уравнения.

Если каждой паре чисел x, y из некоторой области соответствует одно или несколько значений z, которые удовлетворяют уравнению F(x,y,z)=0, то это уравнение неявно определяет одно или несколько значений однозначных функций z от x и y.

Пусть функция y=f(x) определяется уравнением F (x,y)=0

Подставим в F (x,y)=0 вместо y функцию f(x). Тогда F (x,y)=0 превратится в тождество относительно x. Продифференцируем данное тождество. Справа получим 0. Левая часть тождества - это сложная функция от x, обозначим её через z.

z=F(x,y), y=f(x).

По формуле (8) z _x’=F_x’(x,y)x_x’+F_y’(x,y)y_x’.

Учитывая, что x_x’=1, получим F _x’(x,y)+F_y’(x,y)y_x’=0

Отсюда (12)

Рассмотрим уравнение вида F(x,y,z)=0

Найдём частные производные z_x’ и z_y’ неявной функции z от x и y. Прq1 `и вычислении z_x’, y считаем постоянной величиной, поэтому, применив формулу (12), получим

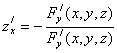(14) Аналогично, (15)

Таким же образом определяются неявные функции любого числа переменных и находятся их частные производные.

Дата добавления: 2015-08-20