
Читайте также:
|
Шесть основных гиперболических функций определяются следующим образом:

| 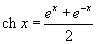
|

| 
|

| 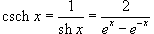
|
Наиболее важные формулы дифференцирования и интегрирования гиперболических функций имеют вид:

| 
|

| 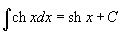
|
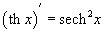
| 
|
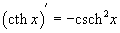
| 
|

| 
|

| 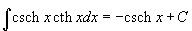
|
Приведем еще несколько полезных соотношений:



Если подынтегральное выражение содержит гиперболическую функцию, то такой интеграл можно свести к интегрированию рациональной функции с помощью подстановки  .
.
Дата добавления: 2015-08-20; просмотров: 189 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование простейших иррациональных алгебраических функций. | | | Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления) |