Аналитическое представление функций

алгебры логики (ФАЛ)

Существует много способов задания логических функций. Нами ранее был рассмотрен табличный способ, при котором каждому набору значений переменных в таблице истинности указывается значение самой логической функции. Этот способ нагляден и может быть применен для записи функций от любого количества переменных. Однако, при анализе свойств ФАЛ такая запись не является компактной. Проще выглядит аналитическая запись в виде формул.

Известны два пути перехода от табличного задания двоичной функции к заданию в виде формулы с использованием функций ОФПС:

1. образование совершенной дизъюнктивной нормальной формы (СДНФ) функции;

2. образование совершенной конъюнктивной нормальной формы (СКНФ) функции.

Совершенной дизъюнктивной нормальной формой двоичной функции называется дизъюнкция (логическая сумма) конституент единицы, соответствующих тем наборам значений аргументов, при которых функция принимает единичное значение.

Каждая конституента единицы, входящая в дизъюнкцию, принимает единичное значение при том наборе значений аргументов, которому она соответствует. При единичном значении хотя бы одного слагаемого дизъюнкция принимает единичное значение.

Следовательно, при любом наборе значений аргументов, которому соответствует конституента единицы, вошедшая в СДЦФ, функция, представленная в виде СДЕФ, принимает единичное значение. При всех остальных наборах значений аргументов, которым нё соответствует ни одна из конституент единицы, вошедших в СДНФ, все слагаемые в логической сумме принимают нулевое значение и, следовательно, функция, представленная в виде СДНФ, принимает нулевое значение.

Пусть имеется двоичная функция трех аргументов

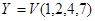
заданная с помощью таблицы

№	Х1	Х2	Х3	Y

Требуется образовать СДНФ функции «Y»

1. Составляем конституенты единицы, соответствующие тем наборам значений аргументов, при которых функция «Y» принимает единичное значение (001, 010, 10О, 111):

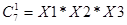
2. Образуем дизъюнкцию составленных конституент единицы и получаем СДНФ функции «Y»:

Функция, заданная приведенной формулой совпадает с функцией, заданной таблицей. Действительно, при нулевом наборе (000) значений аргументов все четыре логических слагаемых л принимают нулевое значение и, следовательно, их логическая сумма равна нулю.

При единичном наборе (001) значений аргументов единичное значение принимает первое слагаемое и, следовательно, логическая сумма принимает единичное значение и т.д.

Проделав подстановку всех наборов значений аргументов в формулу, убеждаемся, что всякий раз, при подстановке набора, которому в таблице соответствует единичное значение функции, функция «Y», заданная формулой, принимает единичное значение, а при подстановки набора, которому соответствует нулевое значение функции, функция принимает нулевое значение.

Формулу для «Y» можно записать еще более компактно если учесть, что конкретные значения аргументов Х_i в таблице (или формуле) можно обозначить через «Х» с двойной индексацией вида:

{

где i= 1, 2, …, n – номер данного аргумента;

j= 0, 1, …, 2ⁿ-1 – номер набора аргументов (строки таблицы)

На основе новых обозначений выражение для f(X1, X2, X3)в общем виде может быть записано как

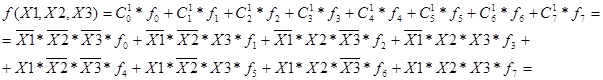
где: – общий знак логической суммы для нескольких аргументов – дизъюнкции;

- общий знак логического произведения для нескольких аргументов – конъюнкции.

{

fj - значение функции на j-ом наборе (0 или 1).

Соотношение () легко доказывается тем же способом, что и () - подстановкой всех возможных (восьми) комбинации значений аргументов. Используя метод математической индукции, можно перейти к общему выражению для логической функции n-аргументов имеем:

Анализ полученного соотношения (1) приводит к важным выводам:

1) поскольку в этом виде (1) можно представить любую таблично заданную функцию любого (конечного) числа аргументов, то существование соотношения () служит доказательством функциональной полноты трех логических связей, используемых этим соотношением: отрицания, конъюнкции и дизъюнкции;

2) каждый член в логической сумме (1) в зависимости от значения

{

обращается либо в нуль, либо в конституенту единицы;

3) количество членов в логической сумме (1) в зависимости от значений fj находится в пределах от 0 до 2ⁿ-1

Два последних соображения приводят к тому, что соотношение (1) можно несколько упростить, поскольку нет смысла записывать те члены (произведения), в которых fj=0. Для этого представим соотношение (1) в виде двух слагаемых следующего вида:

Очевидно, вторая сумма в формуле (2) равна нулю, поэтому окончательно можем записать:

Соотношение (3) позволяет сформулировать правило получения аналитической записи логической функции - для некоторого комбинационного узла ЭЦВМ:

для того чтобы получить аналитическое выражение функции, заданной таблично, в СДНФ нужно составить сумму конституент единицы для тех наборов значений входных двоичных переменных, для которых реализации функции fj равны 1, причем символ любой переменной в некоторой конституенте берется со знаком отрицания, если конкретное значение переменной.[Xi]j в рассматриваемом наборе имеет значение "0".

Пример: Составить логические функции, описывающие работу полусумматора, пользуясь табл. 1

Решение: Пользуясь сформулированным правилом и табл. 1, записываем искомые аналитические выражения:

} ()

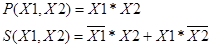Все функции, полученные в соответствии с формулой (), независимо от числа аргументов имеют много общего в своей структуре туре. Используя законы алгебры логики или их следствия, можно эту структуру значительно видоизменить. От любого вида логической функции можно снова перейти к сумме конституент единицы (например, через таблицу истинности). Таким образом, полученное соотношение (3) определяет канонический вид любой логической функции. В этом случае говорят, что, функция задана (записана) в совершенной дизъюнктивной нормальной форме (СДНФ).

Нормальной эта форма называется потому, что члены функции в данном случае имеют вид элементарных конъюнкций.

Вследствие того, что все члены соединены в одну функцию знаком дизъюнкции, форма носит название дизъюнктивной.

Форма называется совершенной, так как все члены имеют высший ранг, являясь конституентами единицы.

Действительно поскольку алгебра логики симметрична, то возможна еще одна каноническая форма логических функций – в виде совокупности конституент нуля, соединенных знаком конъюнкции. Применив методику вывода, использованную для получения соотношения (3), получим следующее выражение

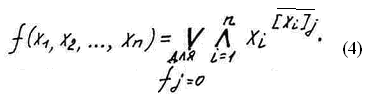
Если функция построена в соответствии с формулой (4), то говорят, что она имеет совершенную конъюнктивную нормальную форму (СКНФ).

Сформулируем второе правило получения аналитической записи логической функции, заданной таблично, пользуясь соотношением (4):

Для того чтобы получить аналитическое выражение функции, заданной таблично, в СКНФ, необходимо составить логическое произведение конституент нуля, для тех наборов значений входных двоичных переменных, для которых реализация функции fj равна "0", причем символ любой переменной в некоторой конституенте берется со знаком отрицания, если ее конкретное значение [Xi]j в рассматриваемом наборе равно "1", и без отрицания если – "0".

Пример: Составить в СКНФ логические функции, описывающие работу полусумматора.

Решение. Пользуясь сформулированным правилом и табл., записываем:

} ()

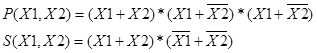Поскольку логическая сумма всех элементарных произведений ' наивысшего ранга n обязательно равна "1, какой бы набор значений входных переменных ни рассматривался, то эти произведения вполне логично называть конституентами (составляющими) единицы.

Аналогично объясняется и название конституенты (составляющей) нуля, так как известно, что логическое произведение всех элементарных сумм наивысшего ранта тождественно равно нулю.

Числовое представление ФАЛ.

Для компактной записи ФАЛ вместо полного перечисления конституент единицы (нуля) используются номера, для которых функция принимает единичное (нулевое) значение.

Например, функция, заданная таблицей (табл.)

№	Х1	Х2	Х3	Y

может быть записана

или

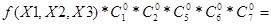
Это означает, что функция принимает значение "1" на наборах, номера которых равны 0,3 и 4 или - принимает значение "0" на наборах, номера которых равны 1,2,5,6,7.

Такую форму записи называют числовой.

---

Дата добавления: 2015-08-17