Итегральное преобразование Фурье. Спектральная плотность сигналов и ее свойства.

Сигналы связи всегда ограничены во времени и поэтому не являются периодическими. Среди непериодических сигналов наибольший интерес представляют одиночные импульсы (ОИ). ОИ можно рассматривать как предельный случай периодической последовательности импульсов (ППИ) длительностью 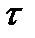при бесконечно большом периоде их повторения .

Т

t

t

τ

τ

Рисунок 6.1 – ППИ и ОИ.

Непериодический сигнал может быть представлен суммой бесконечно большого числа бесконечно близких по частоте колебаний с исчезающе малыми амплитудами. Спектр ОИ является непрерывным и вводится интегралами Фурье:

- (1) - прямое преобразование Фурье. Позволяет аналитически отыскать спектральную функцию по заданной форме сигнала;

- (2) - обратное преобразование Фурье. Позволяет аналитически отыскать форму по заданной спектральной функции сигнала.

Комплексная форма интегрального преобразования фурье (2) дает двустороннее спектральное представление (имеющее отрицательные частоты) непериодического сигнала 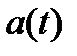в виде суммы гармонических колебаний с бесконечно малыми комплексными амплитудами , частоты которых непрерывно заполняют всю ось частот.

- комплексная спектральная плотность сигнала – комплексная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных гармоник.

Поскольку для представления спектров непериодических сигналов используются интегральные преобразования Фурье, эти спектры сплошные.

Спектральная плотность может быть представлена в виде:

Вещественная часть спектральной плотности есть чётная функция частоты:

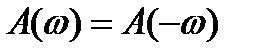
Мнимая часть спектральной плотности есть нечётная функция частоты:

Если записать спектральную плотность в показательной форме, то можно выделить её модуль и аргумент:

Модуль спектральной плотности называется амплитудным спектром сигнала:

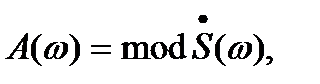
а аргумент спектральной плотности – фазовым спектром сигнала.

Пара преобразований Фурье имеет фундаментальное значение в теории электросвязи, так как многие характеристики сигналов связаны между собой этими преобразованиями.

Все свойства спектральной плотности объединены в основных теоремах о спектрах.

Преобразуем формулу (2):

Тригонометрическая форма интегрального преобразования фурье дает одностороннее спектральное представление (не имеющее отрицательных частот) непериодического сигнала:

.

Дата добавления: 2015-08-20