Читайте также:
|
Взаимокорреляционной функцией (ВКФ) двух вещественных сигналов U(t) и V(t) называется скалярное произведение вида:
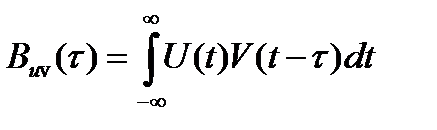(4.18)
ВКФ служит мерой «устойчивости» ортогонального состояния при сдвигах сигналов во времени.
Действительно, если сигналы U(t) и V(t) ортогональны в исходном состоянии, то 
При прохождении этих сигналов через различные устройства возможно, что сигнал V(t) будет сдвинут относительно сигнала U(t) на некоторое время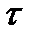 
.
Свойства ВКФ.
1) В отличие от АКФ одиночного сигнала, ВКФ, описывающая свойства системы двух независимых сигналов, не является чётной функцией аргумента :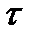
(4.19)
2) Если рассматриваемые сигналы имеют конечные энергии, то их ВКФ ограничена.
3) При 
значения ВКФ вовсе не обязаны достигать максимума.
Пример ВКФ может служить
взаимокорреляционная функция прямоугольного и треугольного видеоимпульсов.
Установим связь ВКФ со взаимной спектральной плотностью (взаимным энергетическим спектром)
На основании теоремы Планшереля
и поскольку спектр смещённого во времени сигнала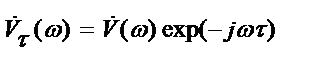 
,то 
и 
(4.20)
Поскольку 
взаимный энергетический спектр то будет справедливо равенство:
(4.21)
Таким образом, взаимокорреляционная функция и взаимный энергетический спектр связаны между собой парой преобразований Фурье.
Если сигналы U(t) и V(t) – дискретные, то их можно задать как совокупность отсчётов, следующих во времени с одинаковыми интервалами T
Тогда по аналогии с АКФ одиночного сигнала ВКФ двух дискретных сигналов определится по формуле:
(4.22)
где n – целое число, положительное, отрицательное или нуль.
Дата добавления: 2015-08-20; просмотров: 207 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Автокорреляционная функция сигналов | | | Сигналы и векторы. |