Теоремы о спектрах. Свойство линейности.Если имеется некоторая совокупность сигналов причём ,

Свойство линейности. Если имеется некоторая совокупность сигналов 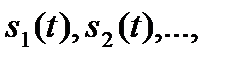причём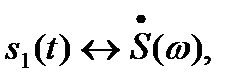 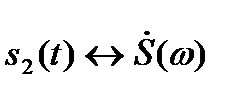,…, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:

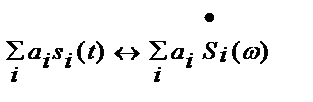(2.11)

Здесь 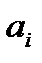- произвольные числовые коэффициенты.

Теорема о сдвигах.

Предположим, что для сигнала 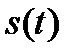известно соответствие . Рассмотрим такой же сигнал, но возникающий на 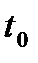секунд позднее. Принимая точку 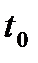за новое начало отсчёта времени, обозначим этот смещённый сигнал как 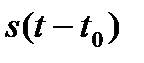. Введём замену переменной: 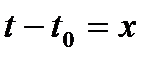. Тогда ,

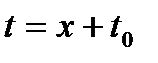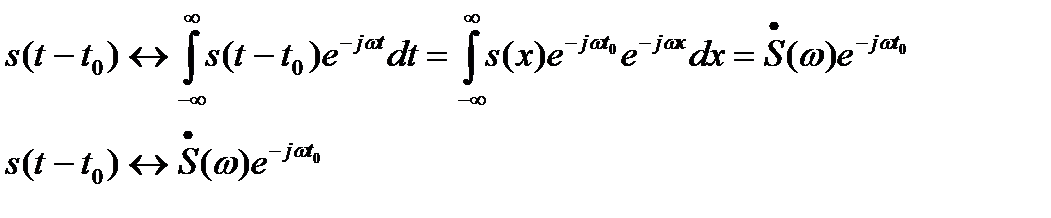
Модуль комплексного числа 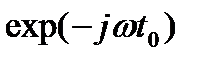при любых 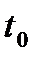равен 1, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена в частотой зависимости аргумента от его спектральной плотности (фазовом спектре).

Теорема масштабов.

Предположим, что исходный сигнал 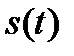подвергнут изменению масштаба времени. Это означает, что роль времени играет новая независимая переменная ( 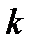- некоторое вещественное число.) Если 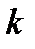> 1, то происходит “ сжатие” исходного сигнала; если же 0< 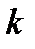<1, то сигнал “растягивается” во времени. Если 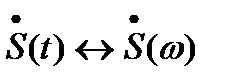, то:

Произведём замену переменной 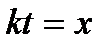, тогда 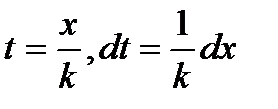, откуда следует:

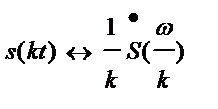(2.13)

При сжатии сигнала в 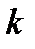раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в 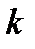раз.

Очевидно, что при растягивании сигнала во времени (т.е. при 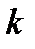<1) имеет место сужение спектра и увеличение модуля спектральной плотности.

Дата добавления: 2015-08-20