
Читайте также:
|
По определению, дельта-функция описывается следующими математическими выражениями (в совокупности):
d(t-t) = 0 при t ¹t,
 d(t-t) dt = 1.
d(t-t) dt = 1.
Функция d(t-t) не является дифференцируемой, и имеет размерность, обратную размерности ее аргумента, что следует из безразмерности результата интегрирования. Значение дельта-функции равно нулю везде за исключением точки t, где она представляет собой бесконечно узкий импульс с бесконечно большой амплитудой, при этом площадь импульса равна 1.
Дельта-функция является полезной математической абстракцией. На практике такие функции не могут быть реализованы с абсолютной точностью, так как невозможно реализовать значение, равное бесконечности, в точке t = t на аналоговой временной шкале. Но во всех случаях, когда площадь импульса равна 1, длительность импульса достаточно мала, а за время его действия на входе системы сигнал на ее выходе практически не изменяется (реакция системы на импульс во много раз больше длительности самого импульса), входной сигнал можно считать единичной импульсной функцией со свойствами дельта - функции.
При своей абстрактности дельта - функция имеет вполне определенный физический смысл. Представим себе импульсный сигнал прямоугольной формы П(t-t) длительностью q, амплитуда которого равна 1/q, а площадь соответственно равна 1. При уменьшении значения длительности q импульс, сокращаясь по длительности, сохраняет свою площадь, равную 1, и возрастает по амплитуде. Предел такой операции при qÞ 0 и носит название дельта - импульса. Этот сигнал d(t-t) сосредоточен в одной координатной точке t = tконкретное амплитудное значение сигнала не определено, но площадь (интеграл) остается равной 1. Это не мгновенное значение функции в точке t = t, а именно импульс (импульс силы в механике, импульс тока в электротехнике и т.п.) – математическая модель короткого действия, значение которого равно 1.
Дельта-функция обладает фильтрующим свойством. Суть его заключается в том, что если дельта-функция d(t-t) входит под интеграл какой-либо функции в качестве множителя, то результат интегрирования равен значению подынтегральной функции в точке t расположения дельта-импульса, т.е.:
 s(t) d(t-t) dt = s(t).Интегрирование в выражении может ограничиваться ближними окрестностями точки t.
s(t) d(t-t) dt = s(t).Интегрирование в выражении может ограничиваться ближними окрестностями точки t.
3.Понятия мощности и энергии в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.
Для произвольного, в общем случае комплексного, сигнала s(t) = a(t)+jb(t), где а(t) и b(t) - вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:
w(t) = s(t) s*(t) = [a(t)+jb(t)] [a(t)-jb(t)] = a2(t)+b2(t) = |s(t)|2, (2.2.1)
т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов - квадрату функции амплитуд.
Аналогично для дискретных сигналов:
wn = sns*n = [an+jbn] [an-jbn] = an2 + bn2 = |sn|2, (2.2.1')
Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:
Еs=  w(t)dt =
w(t)dt =  |s(t)|2dt. (2.2.2)
|s(t)|2dt. (2.2.2)
Es =  wn =
wn =  |sn|2. (2.2.2')
|sn|2. (2.2.2')
Мгновенная мощность w(t) является плотностью мощности сигнала, так как измерения мощности возможны только через энергию на интервалах ненулевой длины:
w() = (1/t) 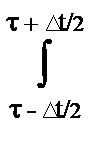 |s(t)|2dt
|s(t)|2dt
Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.
Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов - в пределах одного периода Т, при этом средняя мощность (average power) сигнала:
WT() = (1/T) 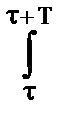 w(t) dt= (1/T)
w(t) dt= (1/T) 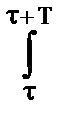 |s(t)|2 dt. (2.2.3)
|s(t)|2 dt. (2.2.3)
Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:
Ws = 
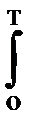 w(t) dt. (2.2.3')
w(t) dt. (2.2.3')
Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала (root mean sqare, RMS).
Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):
w(t) = |s(t)|2/R,
а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности, и могут быть формализованным отображением любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой метрологические характеристики сигналов.
Из сравнения выражений (2.1.2) и (2.2.2) следует, что энергия и норма сигнала связаны соотношениями:
Es = ||s(t)||2, ||s(t)|| =  (2.2.4)
(2.2.4)
Пример. Цифровой сигнал задан функцией s(n) = {0,1,2,3,4,5,4,3,2,1,0,0,0,0....}.
Энергия сигнала: Es = 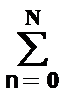 s2(n) = 1+4+9+16+25+16+9+4+1 = 85.
s2(n) = 1+4+9+16+25+16+9+4+1 = 85.
Норма: ||s(n)|| =  » 9.22
» 9.22
Вычислим энергию суммы двух произвольных сигналов u(t) и v(t):
E =  [u(t)+v(t)]2 dt = Eu + Ev + 2
[u(t)+v(t)]2 dt = Eu + Ev + 2  u(t)v(t) dt. (2.2.5)
u(t)v(t) dt. (2.2.5)
4 Обобщенный ряд Фурье. Базисные функции. Отронормированный базис.
Введём понятие скалярного произведения элементов линейного пространства. Скалярное произведение вещественных сигналов u и v:
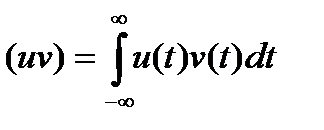 (1.6)
(1.6)
Скалярное произведение обладает следующими свойствами:
1. 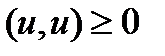
2. 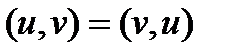
3.  , где
, где  - вещественное число
- вещественное число
4. 
5. 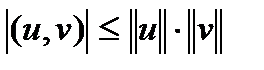 - справедливо неравенство Коши-Буняковского.
- справедливо неравенство Коши-Буняковского.
Линейное пространство с таким скалярным произведением, содержащее в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства называется вещественным Гильбертовым пространством H.
Если сигналы принимают комплексные значения, то можно определить комплексное Гильбертово пространство.
Если сигналы комплексные, то скалярное произведение:
 (1.7)
(1.7)
Два сигнала  и
и  называют ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:
называют ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:
 (1.8)
(1.8)
Предположим, что на отрезке  задана бесконечная система функций
задана бесконечная система функций  , ортогональных друг другу и обладающих единичными нормами:
, ортогональных друг другу и обладающих единичными нормами:
 1, если
1, если 
0, если 
Говорят, что при этом в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал 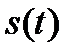 в ряд:
в ряд:
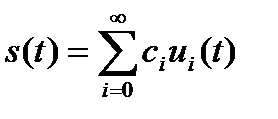 (1.10)
(1.10)
Такое представление называется обобщённым рядом Фурье сигнала  в выбранном базисе.
в выбранном базисе.
Коэффициенты данного ряда находят следующим образом. Возьмём базисную функцию 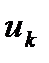 с произвольным номером
с произвольным номером  , умножим на неё обе части равенства (1.10) и затем проинтегрируем результаты по времени:
, умножим на неё обе части равенства (1.10) и затем проинтегрируем результаты по времени:
 (1.11)
(1.11)
Ввиду ортонормированности базиса по определению в правой части равенства (1.11) останется только член суммы с номером  , поэтому:
, поэтому:
 (1.12)
(1.12)
Рассмотрим некоторый сигнал,  , разложенный в ряд по ортонормированной базисной системе и вычислим его энергию, непосредственно подставив этот ряд в соответствующий интеграл:
, разложенный в ряд по ортонормированной базисной системе и вычислим его энергию, непосредственно подставив этот ряд в соответствующий интеграл:
 (1.13)
(1.13)
Поскольку базисная система функций ортонормирована, в сумме (1.13) отличными от нуля окажутся только члены с номерами  . Отсюда получается замечательный результат, который называется равенством Парсеваля:
. Отсюда получается замечательный результат, который называется равенством Парсеваля:
 (1.14)
(1.14)
Смысл этой формулы: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщённый ряд Фурье.
Эта теорема (доказана академиком Котельниковым В.А. в 1933 г.), устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром, исходя из отсчетных значений (выборок), взятых через равные промежутки времени.
Любые два сигнала с ограниченным спектром, принадлежащие семейству 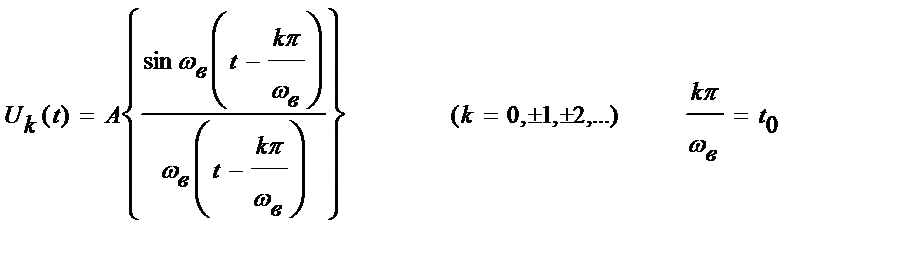 (3.9)
(3.9)
являются ортогональными если установить сдвиг 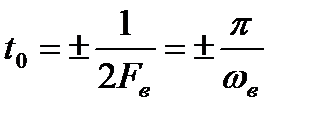
Путём соответствующего выбора амплитудного множителя А можно добиться того, чтобы норма каждого из этих сигналов стала единичной. В результате будет построен ортонормированный базис, позволяющий разложить произвольный сигнал с ограниченным спектром в обобщённый ряд Фурье. Из семейства функции  достаточно рассмотреть лишь функцию
достаточно рассмотреть лишь функцию  при k=0.
при k=0.
 (3.10)
(3.10)
так как норма любого сигнала  одинакова независимо от сдвига во времени. Определим квадрат нормы
одинакова независимо от сдвига во времени. Определим квадрат нормы  и проинтегрируем по t.
и проинтегрируем по t.

Функции  будут ортонормированными, если:
будут ортонормированными, если:
 (3.11)
(3.11)
Бесконечная совокупность функций.
 (3.12)
(3.12)
образует базис Котельникова в линейном пространстве низкочастотных сигналов со спектрами, ограниченными сверху значением  . Отдельная функция
. Отдельная функция  называется k-той отсчётной функцией. Если
называется k-той отсчётной функцией. Если 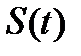 произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот
произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот  то его можно разложить в обобщенный ряд Фурье по базису Котельникова:
то его можно разложить в обобщенный ряд Фурье по базису Котельникова:
 (3.13)
(3.13)
Коэффициентами ряда служат, как известно, скалярные произведения разлагаемого сигнала и k-той отсчётной функции:
 .14)
.14)
Удобный способ вычисления этих коэффициентов заключается в применении теоремы Планшереля. Легко проверить, что каждая отсчётная функция в пределах отрезка  имеет спектральную плотность, равную
имеет спектральную плотность, равную  .
.
Тогда, если  - спектр излучаемого сигнала S(t), то по теореме Планшереля
- спектр излучаемого сигнала S(t), то по теореме Планшереля  ,
,
Тогда:
 (3.15)
(3.15)
Величина в фигурных скобках есть не что иное, как 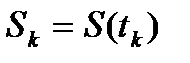 , т.е. мгновенное значение сигнала S(t) в каждой отсчётной точке
, т.е. мгновенное значение сигнала S(t) в каждой отсчётной точке  (по аналогии с
(по аналогии с  )
)
Таким образом:
 (3.16)
(3.16)
Откуда следует выражение ряда Котельникова:

Теорему Котельникова принято формулировать так: произвольный сигнал, спектр которого не содержит частот выше  Гц, может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени
Гц, может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени  с.
с.
Важная особенность теоремы Котельникова состоит в её конструктивном характере: она не только указывает на возможность разложения сигнала в соответствующий ряд, но и определяет способ восстановления непрерывного сигнала, заданного своими отсчётными значениями.
Теорема Котельникова показывает возможность «цифровизации» непрерывных сообщений.
Для представления непрерывных сигналов используются различные системы ортогональных функций.
I. Для представления непрерывных сигналов используются преимущественно ортогональные функции и полиномы Лежандра, Чебышева, Лагерра и Эрмита.
1) Полиномы Лежандра (1-го рода) определяются формулой:
 ,
,
Ряд выглядит следующим образом:
 Спектральные коэффициенты
Спектральные коэффициенты  определяются формулой:
определяются формулой:
 ,
,
2) Полиномы Чебышева (1-го рода) определяются формулой:

Ряд:

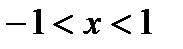

График полинома Чебышева 4-го порядка:
Полиномы Чебышева обеспечивают наименьшую максимальную ошибку аппроксимации на интервале 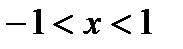 . Эффективны для аппроксимации АЧХ различных фильтров.
. Эффективны для аппроксимации АЧХ различных фильтров.
3) Полиномы Лагерра определяются формулой
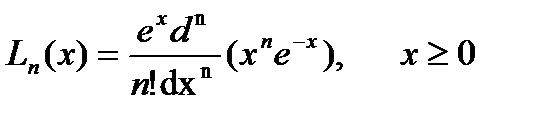
Так как полиномы Лагерра образуют систему расходящихся при  функций, то удобнее пользоваться функциями Лагерра
функций, то удобнее пользоваться функциями Лагерра
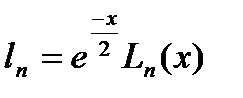
Разложение в ряд по функциям Лагерра

коэффициенты должны определяться по формуле:

Функции Лагерра получили широкое распространение в измерительной технике и в многоканальных системах связи, что объясняется простотой их генерирования.
4) Полиномы Эрмита определяются формулой:
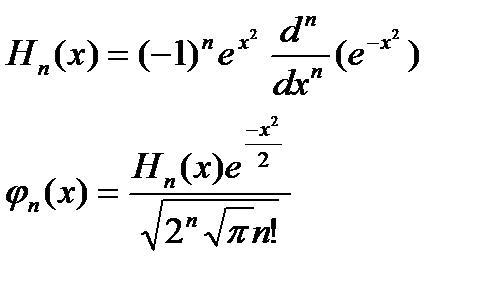
Разложение в ряд по нормированным функциям Эрмита:

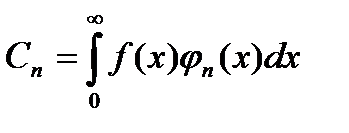 - коэффициенты ряда (спектральные составляющие)
- коэффициенты ряда (спектральные составляющие)
Полиномы Эрмита отличаются от полиномов Лагерра тем, что полиномы Лагерра определены на интервале, представляющем собой полуось  , а полиномы Эрмита – на интервале, представляющем собой всю ось
, а полиномы Эрмита – на интервале, представляющем собой всю ось  .
.
Дата добавления: 2015-08-20; просмотров: 348 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация сигналов | | | Функции Уолша и их свойства |