Сигналы и векторы.

Аналоговый сигнал s (t), подвергшийся дискретизации на временном интервале [ a, b ] можно записать в виде ряда значений N точек (которые мы так же называли отсчетами):

S = (s ₀, s ₁, s ₂,..., s_{N -1})

Данный ряд можно представить N -мерным вектором (величиной представленной набором N числовых значений, расположенных в определенном порядке). Условимся здесь и далее обозначать вектор жирным шрифтом - S. Элемент из этого числового набора называется компонентой вектора. Качество приближения функции s (t) (рисунок 1 а) вектором S зависит от числа N (очевидно, что при фиксированном интервале [ a, b ] изменение N влияет на период дискретизации T) (рисунок 1 б,в). При N →∞ (а значит при T →0), вся информация, содержащаяся в исходном сигнале s (t) на временном интервале [ a, b ] (если сигнал s (t) не имеет на данном интервале точек разрыва) будет содержаться и в векторе S (рисунок 1 г). Это означает, что анализ вектора S будет равнозначен анализу исходного аналогового сигнала на интервале [ a, b ], заданного функцией s (t).

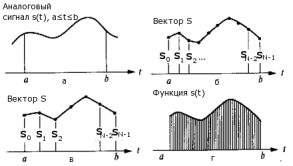
Рисунок 1

Двумерный вектор, расположенный в двумерном пространстве (на плоскости), соответствует одной точке на этой плоскости (графически представляется отрезком, соединяющим начало координат и заданную точку, стрелочкой указывается направление). Трехмерный вектор соответствует точке в трехмерном пространстве, N - мерный вектор так же соответствует точке, но в N -мерном пространстве, которое к сожалению (или к счастью) мы не можем представить графически. Если представить пространство бесконечно большой размерности, то непрерывная функция s (t) соответствует одной точке этого пространства. Это абстрактное пространство бесконечной размерности называют пространством функций.

Множество сигналов 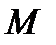образует вещественное линейное пространство, если справедливы следующие аксиомы:

1. Любой сигнал при любых принимает лишь вещественные значения.

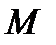2. Для любых и существует их сумма , причём также содержится в . Операция суммирования коммутативна: и ассоциативна .

3. Для любого сигнала 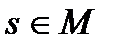и любого вещественного числа определён сигнал .

4. Множество 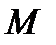содержит особый нулевой элемент 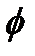, такой, что 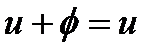для всех .

Линейное пространство, элементами которого являются функции, называется функциональным.

Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, можем ввести понятие комплексного линейного пространства.

Как и в обычном трёхмерном пространстве в линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. В качестве таких осей используются линейно независимые векторы.

Совокупность векторов ,принадлежащих , является линейно независимой, если равенство:

(1.1)

возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов .

Система линейно независимых векторов образует координатный базис в линейном пространстве.

Аксиомы нормированного пространства

1. Норма неотрицательна, т.е. . Норма =0 тогда и только тогда, если

2. Для любого числа справедливо равенство .

3. Если и 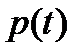- два вектора из L, то выполняется неравенство:

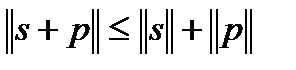
Существуют разные способы определения нормы сигналов. Чаще всего полагают, что вещественные аналоговые сигналы имеют норму:

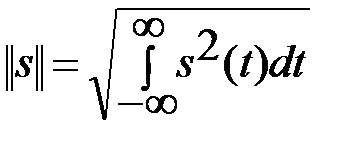(1.2)

(из двух возможных значений корня выбирается положительное). Для комплексных сигналов норма:

,

где *-символ комплексно-сопряжённой величины.

Квадрат нормы называется энергией сигнала

(1.3)

Такая энергия выделяется в резисторе с сопротивлением 1Ом, если на его зажимах существует напряжение .

Норму в свою очередь, можно понимать как расстояние между выбранным элементом пространства и нулевым элементом: .

Дата добавления: 2015-08-20