Теоремы о спектрах

Теорема о свёртке.

Как известно, при суммировании сигналов их спектры складываются. Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей.

Пусть 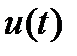и 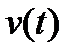- два сигнала, для которых известны соответствия 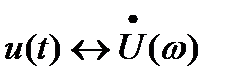, .Образуем произведение этих сигналов: и вычислим его спектральную плотность. По общему правилу:

(2.18)

Применив обратное преобразование Фурье, выразим сигнал через его спектральную плотность и подставим результат в (2.18):

Изменив порядок интегрирования, будем иметь:

откуда:

(2.19)

Интеграл, стоящий в правой части называют свёрткой функций V и U. Символически операция свёртки обозначается как *

Таким образом, спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свёртке спектральных плотностей сомножителей:

(2.20)

Операция свёртки коммутативна, т.е. допускает изменения порядка следования преобразуемых функций:

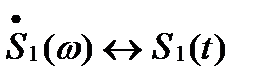Теорема о свёртке может быть обращена: если спектральная плотность некоторого сигнала представляется в виде произведения , причём и 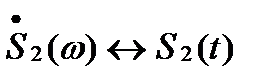, то сигнал является свёрткой сигналов и , но уже не в частной, а во временной области:

(2.21)

Теорема Планшереля

Пусть два сигнала и , в общем случае комплексные, определены своими обратными преобразованиями Фурье:

;

.

Найдём скалярное произведение этих сигналов, выразив один из них, например , через его спектральную плотность:

Здесь внутренний интеграл представляет собой спектральную плотность сигнала поэтому:

(2.22)

Скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей.

Дата добавления: 2015-08-20