Автокорреляционная функция сигналов

Задача корреляционного анализа возникла из радиолокации, когда нужно было сравнить одинаковые сигналы, смещённые во времени.

Для количественного определения степени отличия сигнала U(t) и его смещённой во времени копии принято вводить автокорреляционную функцию (АКФ) сигнала U(t), равную скалярному произведению сигнала и его сдвинутой копии.

(4.8)

Свойства АКФ

1) При автокорреляционная функция становится равной энергии сигнала:

(4.9)

2) АКФ – функция чётна

(4.10)

3) Важное свойство автокорреляционной функции состоит в следующем: при любом значении временного сдвига модуль АКФ не превосходит энергии сигнала:

4) Обычно, АКФ представляется симметричной линей с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала U(t) автокорреляционная функция может иметь как монотонно убывающей, так и колеблющийся характер.

Например:

АКФ прямоугольного видеоимпульса

АКФ пачки из трёх прямоугольных видеоимпульсов, сдвинутых друг относительно друга на время T.

АКФ бесконечной периодической последовательности видеоимпульсов:

Существует тесная связь между АКФ и энергетическим спектром сигнала.

В соответствии с формулой (4.8) АКФ есть скалярное произведение . Здесь символом обозначена смещённая во времени копия сигнала .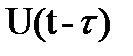

Обратившись к теореме Планшереля – можно записать равенство:

Спектральная плотность смещённого во времени сигнала 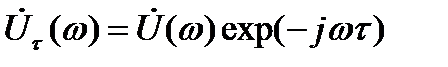, откуда . Таким образом приходим к результату

(4.12)

Квадрат модуля спектральной плотности представляет собой энергетический спектр сигнала. Итак энергетический спектр и автокорреляционная функция связаны парой преобразований Фурье.

Ясно что имеется и обратное соотношение

(4.13)

Эти результаты принципиально важны по двум причинам: во-первых оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Во-вторых, формулы (4.12), (4.13) указывают путь экспериментального определения энергетического спектра. Часто удобнее вначале получить АКФ, а затем, используя преобразование Фурье, найти энергетический спектр сигнала. Такой приём получил распространение при исследовании свойств сигналов с помощью быстродействующих ЭВМ в реальном масштабе времени.

Часто вводят удодный числовой параметр – интервал корреляции , представляющий собой оценку ширины основного лепестка АКФ.

Например:

В данном случае:

Отсюда: (4.14)

Интервал корреляции тем меньше, чем выше верхняя граничная частота спектра сигнала. (Чем шире полоса частот сигнала тем уже основной лепесток АКФ.)

АКФ дискретного сигнала

Важнейшая операция при обработке дискретных сигналов состоит в сдвиге такого сигнала на некоторое число позиций относительно исходного положения без изменения его формы. В качестве примера приведём некоторый исходный сигнал (первая строка) и его копии (последующие строки), сдвинутые на 1,2 и 3 позиции в сторону запаздывания.

…………………………..00011110000…………………

…………………………..00001111000…………………

…………………………..00000111100…………………

…………………………..00000011110…………………

Обобщим формулу (4.8), чтобы можно было вычислять дискретный аналог АКФ применительно к многопозиционным сигналам. Операцию интегрирования следует заменить суммированием, а вместо переменной использовать целое число n (положительное или отрицательное), указывающее, на сколько позиций сдвинута копия относительно исходного сигнала. Так как в «пустых»позициях математическая модель сигнала содержит нули, запишем дискретную АКФ в виде:

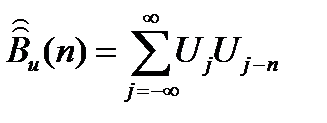(4.15)

Эта функция целочисленного аргумента n естественно обладает многими уже известными свойствами обычной АКФ. Так, дискретная АКФ чётна:

(4.16)

При нулевом сдвиге эта АКФ определяет энергию дискретного сигнала:

(4.17)

Дата добавления: 2015-08-20