Читайте также:
|
Пусть четырехполюсник является линейным и на его вход подан стационарный случайный процесс с нулевым средним значением. Спектральная плотность этого процесса на входе равна G1(ω), акорреляционная функция — B 1(τ). Коэффициент передачи четырехполюсника равен K (j ω).
Требуется найти корреляционную функцию Β2(τ) и соответствующую ей спектральную плотность мощности случайного процесса G2(ω) на выходе четырехполюсника.
Если на вход подан стационарный случайный процесс с нулевым средним значением, то на выходе установившийся процесс также будет стационарным.
Можно показать, что спектральная плотность мощности входного стационарного случайного процесса определяется также, как и спектральная плотность мощности детерминированного сигнала, т.е.
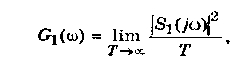(5.17)где 
— спектральная плотность отрезка входного стационарного случайного процесса ξ1(t) в интервале 0-Т.
Спектральная плотность мощности выходного случайного стационарного процесса
так как спектральная плотность отрезка выходной стационарной случайной функции равна
S 2(j ω) = Si(j ω )K(j ω ).
Корреляционная функция случайного процесса на выходе линейного четырехполюсника
Если линейный четырехполюсник задан импульсной характеристикой h (t), то его реакция на входной случайный процесс ξ1(t) может быть вычислена с помощью интеграла Дюамеля
Полагаем, что входной случайный процесс является стационарным. В этом случае при вычислении среднего значения и корреляционной функции можно воспользоваться формулами (4.17), (4.19). Среднее значение
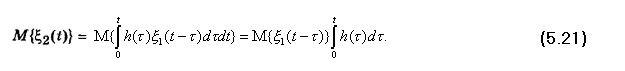
Как следует из (5.21), (5.22), при преобразовании линейным четырехполюсником случайного стационарного процесса он становится нестационарным.
Признаками нестационарности являются: а) зависимость среднего значения от времени; б) зависимость корреляционной функции не от разности t 2 - t1,а от моментов времени t 2 и t1.
Отметим следующие особенности, связанные с прохождением случайных сигналов и помех через линейные системы.
1. Если входной случайный процессξ(t)подчиняется нормальному закону, распределения, то и выходной случайный процесс ξ2(t) также подчиняется нормальному закону.
2. Случайный процесс ξ1(t), подчиняющийся любому закону распределения, при прохождении через линейный четырехполюсник нормализуется, причем закон распределения случайного процесса ξ2(t), тем ближе к нормальному закону, чем уже полоса пропускания этого четырехполюсника.
Дата добавления: 2015-08-20; просмотров: 184 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Гауссовский случайный процесс. Белый шум и его свойства. | | | Воздействие стационарных случайных сигналов на безынерционные нелинейные цепи |