
Читайте также:
|
Задача формулируется следующим образом. Для данной функции распределения w (x 1, x 2,..., xn; t 1, t 2,..., tn) случайной величины ξ1(t) на входе и заданном операторе нелинейного преобразования у = f (x), найти функцию распределения случайной величины ξ2(t) на выходе нелинейного звена системы.
Если функция распределения w(y1,y2,…,yn; t1,...,tn) будет найдена, то по ней нетрудно найти всевозможные статистические характеристики (моменты п -го порядка).
Задача более наглядна и понятна для одномерного случая, когда нелинейный оператор представлен только одним уравнением у = f (x), a плотность распределения вероятности входного случайного процесса ξ1(t) равна w (x).
Пусть существует обратная функция x = φ(у). В этом случае, если случайная величина ξ1находится в пределах x 0<ξ1≤ x 0 + dx, то случайная величина ξ2 будет находиться в пределах у 0<ξ2≤ у 0 + dy (рис.5.8). Вероятность этих событий равны. Поэтому будут равны и заштрихованные площади:
w(x)dx = w(y)dy.
Из полученного равенства находим
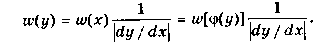
Если известны оператор у = f (x) и двумерная плотность распределения вероятности входного случайного процесса w (x 1, x 2; t 1, t 2), то статистические характеристики случайного процесса (среднее значение и корреляционная функция) определяются по формулам, приведенным ниже.
Среднее значение
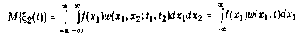
Корреляционная функция
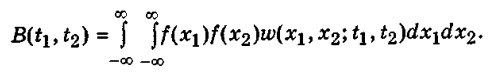
Дата добавления: 2015-08-20; просмотров: 97 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Воздействие случайных сигналов на линейные стационарные цепи | | | Комбинационное разделение сигналов |