Аналитический сигнал.

Анализируя формулу обратного преобразования Фурье, приходим к выводу, что произвольный сигнал S(t) с известной спектральной плотностью можно записать как сумму двух составляющих, каждая из которых содержит или только положительные, или только отрицательные частоты:

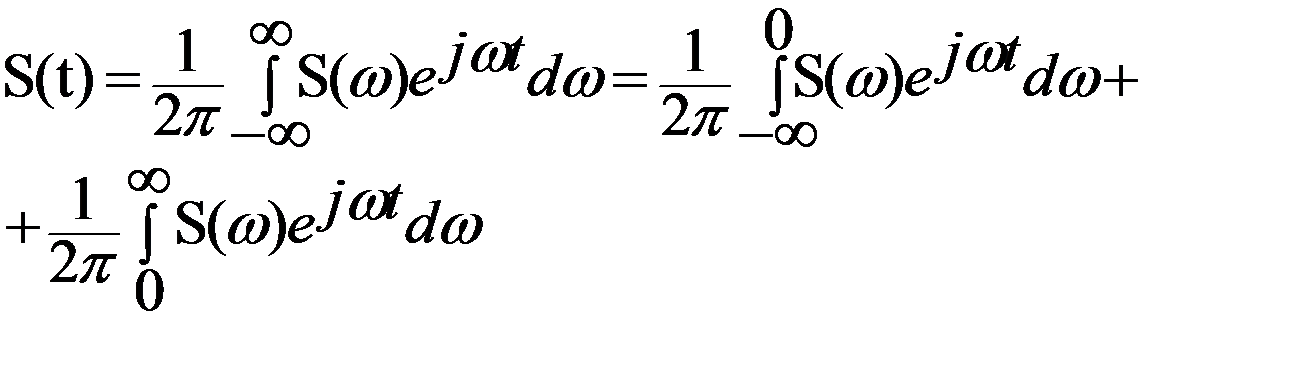(3.26)

Назовём функцию:

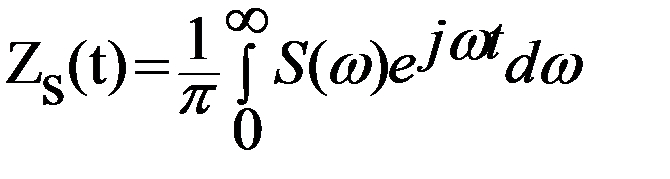(3.27)

аналитическим сигналом, отвечающим колебанию S(t). Первый из интегралов в правой части формулы (3.26) путём замены переменной 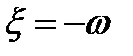преобразуется к виду:

(3.28)

Поэтому формула (3.26) устанавливает связь между сигналами S(t) и 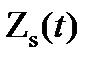: 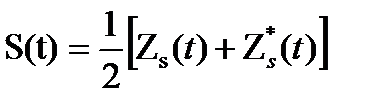(3.29)

или: 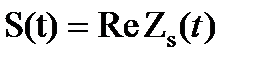- вещественная часть аналитического сигнала. Мнимая часть аналитического сигнала:

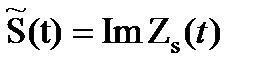(3.30)

Называется сопряжённым сигналом по отношению к исходному колебанию S(t). Итак аналитический сигнал:

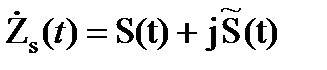(3.31)

На комплексной плоскости этот сигнал отображается вектором, модуль и фазовый угол которого изменяются во времени. Проекция аналитического сигнала на вещественную ось в любой момент времени равна исходному сигналу S(t).

Исследуем спектральную плотность аналитического сигнала. Пусть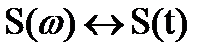

Если 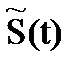- спектральная плотность сопряжённого сигнала, то в силу линейности преобразования Фурье:

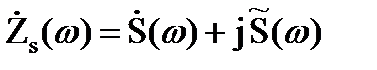(3.32)

Спектральная плотности исходного и сопряжённого сигналов связаны между собой следующим образом:

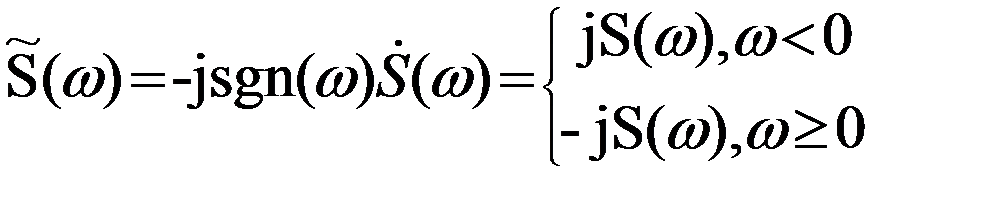(3.33)

Чтобы на практике получить сопряжённый сигнал, необходимо исходное колебание S(t) подать на вход некоторой системы, которая осуществляет поворот фаз всех спектральных составляющих на угол - 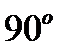в области положительных частот и на угол 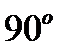в области отрицательных частот, не изменяя по амплитуде. Формула (3.33) показывает, что спектральная плотность сопряжённого сигнала есть произведение спектра 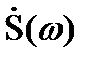исходного сигнала и функции 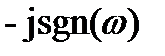. В соответствии с обратной теоремой о свёртке сопряжённый сигнал представляет собой свёртку двух функций S(t) и f(t), которая является обратным преобразованием Фурье по отношении к функции .

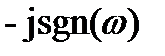Дата добавления: 2015-08-20