|
Читайте также: |
Z-преобразование связано дискретным преобразованием Лапласа посредством подстановки 
.
Z-преобразованием решетчатой функции 
называется функция комплексного аргумента z, определяемая выражением
для смещенной решетчатой функции 
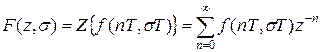
Главное достоинство и удобство z -преобразования заключается в том, что сама запись z -изображения указывает простой способ выполнения прямого и обратного преобразования:
- чтобы по известной функции времени 
найти ее z -изображение, необходимо лишь каждое дискретное значение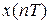 
умножить на 
, а затем свернуть получившийся степенной ряд в конечную сумму;
- чтобы по известному изображению 
найти соответствующий сигнал , необходимо представить изображение в виде степенного ряда по убывающим степеням , получающиеся при этом числовые коэффициенты ряда и есть дискретные значения 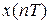сигнала .
Дата добавления: 2015-08-17; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дискретное преобразование Лапласа | | | Отображение p-плоскости на z-плоскость |