Читайте также:
|
Дискретное преобразование Лапласа определяется следующим соотношением:
а) для решетчатой функции 
б) для смещенной решетчатой функции 
где 
- оператор Лапласа;
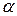- абсцисса абсолютной сходимости.
Для существования изображений по Лапласу 
, 
необходимо, чтобы степенные ряды в выражениях для , сходились. Условием сходимости является 
.
Дискретное преобразование Лапласа содержит трансцендентный сомножитель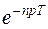 
, из-за которого изображения и соответствующие передаточные функции становятся иррациональными функциями аргумента р, что создает определенные трудности при их использовании. Поэтому с целью получения передаточных функций дискретных систем в дробно-рациональной форме целесообразна определенная замена аргументов (
).
Дата добавления: 2015-08-17; просмотров: 112 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решетчатые функции и разностные уравнения. | | | Z-преобразование |