Отображение p-плоскости на z-плоскость

Связь между комплексной переменной р и комплексной переменной z определяется соотношением , где .

Рассмотрим преобразование плоскости комплексной переменной р в плоскость комплексной переменной z.

Пусть . При изменении от до получаем на плоскости р годограф, совпадающий с осью ординат. Определим, как этот годограф трансформируется на плоскости z. С этой целью зададимся некоторыми значениями частот:

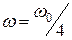, , , , ; , вычислим значения z, нанесем их на плоскость z и сопоставим расположение соответствующих точек на плоскости р и на плоскости z.

1. ; ;

2. ; ;

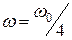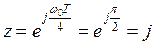3. ; ;

4. ; ;

5. ; ;

Из рисунка видно, что участок мнимой оси плоскости р в интервале от до отображается на плоскости z в окружность единичного радиуса с центром в начале координат. Дальнейший анализ показывает, что участки мнимой оси плоскости р на интервалах до , от до и т.д., т.е. на интервалах, кратных 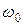, будут отображаться на плоскости z в туже окружность единичного радиуса, причем, левая полуплоскость плоскости р будет отображаться на плоскости z во внутреннюю часть круга единичного радиуса.

Дата добавления: 2015-08-17