Решетчатые функции и разностные уравнения.

Величины, описывающие поведение автоматических систем, представляют собой функции времени. Математическое исследование дискретных систем существенно упрощается в том случае, когда все величины рассматриваются в дискретные равноотстоящие моменты времени.

Решетчатая функциявремени 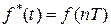, или в сокращенной записи - это математическая функция,значения которой определены в дискретные равноотстоящие друг от другамоменты времени ,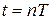

где n - целое положительное число 0, 1, 2...,

Т -период дискретности.

То есть решетчатая функция представляет собой числовую последовательность:

, , , , …,

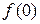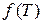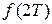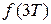Если период дискретности T задан, то решетчатая функция 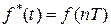однозначно формируется из исходной непрерывной 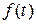. Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками 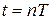, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.Непрерывные функции, проходящие через дискреты заданной решетчатой функции, называют огибающими. Их бесконечно много (рис.21.3).

Для суждения о характере поведения непрерывной функции в интервалах между дискретными моментами времени 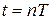водится понятие смещенной решетчатой функции 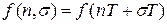, которая представляет собой числовуюпоследовательность:

, , , , …, ,

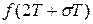где 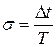- постоянное число, называемое смещением, выбираемое из интервала .

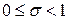Для удобства записи вводят переменную – относительное время . В этом случае непрерывной функции в относительном времени будет соответствовать решетчатая функция или смещенная решетчатая функция , обозначаемая сокращенно .

Аналогами производных и интегралов непрерывных функций для решетчатых функций являются конечные разности и конечные суммы.

Конечные разности решетчатых функций бывают двух видов: прямые(упреждающие) и обратные (отстающие).

Первой прямой конечной разностью функции называется решетчатая функция вида .

Перваяобратная конечная разность .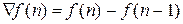

Вторую прямую конечную разность определяют как разность двух первых разностей .

Вторая обратная конечная разность .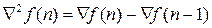

Разности произвольного порядка k определяются при помощи рекуррентных соотношений:

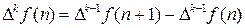
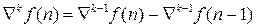
где k = 1, 2, 3,........

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

где z_i - корни характеристического уравнения

C_i - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, -преобразование, а также частотные методы.

Дата добавления: 2015-08-17