Билинейное w -преобразование осуществляется путем замены переменной z и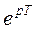 
в z – изображениях или дискретных изображениях по Лапласу:
.
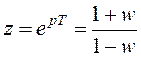Если W(z) есть отношение двух полиномов от z, то W(w) также получится в виде отношения двух полиномов от w.
w -преобразование представляет собой отображение области внутри круга единичного радиуса плоскости z в левую полуплоскость плоскости w, обладающую теми же свойствами, что и левая полуплоскость плоскости р. Данная особенность w -преобразования позволяет применять в исследовании дискретных систем логарифмические частотные характеристики, алгебраические и частотные критерии устойчивости, в том виде, как они сформулированы для непрерывных систем.
Дата добавления: 2015-08-17; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Отображение p-плоскости на z-плоскость | | | Получение разностных уравнений |