Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Б) Найдите площадь сечения.

Читайте также:
  1. B. Найдите к словам в колонке А антонимы из колонки В.
  2. Cравнение отопительных систем среднеутепленного здания площадью 400 м2 (ориентировочно, 2009 год) в зависимости от вида топлива.
  3. IV. Найдите русский эквивалент, соответствующий следующим предложениям.
  4. IV.Найдите в правой колонке русский эквивалент, соответствующий предложению в левой колонке.
  5. Lt;question> Найдите предложение с речевой ошибкой
  6. Oslash; Площадь боковой поверхности

В-81 № 16

В правильной треугольной призме АВСА1В1С1 все рёбра равны 1. Точка Е – середина ребра АС.

А) Постройте сечение призмы плоскостью А1В1Е.

Б) Найдите площадь сечения.

Ответ: 3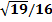

В-90 № 16

В основании прямоугольного параллелепипеда АВСDА1В1С1D1 лежит квадрат АВСD со стороной, равной 3. Боковое ребро параллелепипеда равно 4. На ребре АА1 отмечена точка М так, что АМ:А1М=1:3.

А) Постройте сечение параллелепипеда плоскостью ВМD1.

Б) Найдите площадь сечения.

Ответ: 3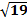

http://reshuege.ru/

3. C 2 № 500193. Точка 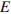— се­ре­ди­на ребра куба Най­ди­те пло­щадь се­че­ния куба плос­ко­стью если ребра куба равны

Ответ: 4,5.

4. C 2 № 500474. Точка 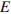— се­ре­ди­на ребра куба Най­ди­те пло­щадь се­че­ния куба плос­ко­стью если ребра куба равны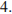

Ответ:

5. C 2 № 500639. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны ребер АВ и ВС и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если все ребра пи­ра­ми­ды равны 8.

Ответ: .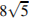

6. C 2 № 500643. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де 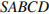с ос­но­ва­ни­ем про­ве­де­но се­че­ние через се­ре­ди­ны рёбер и и вер­ши­ну Най­ди­те пло­щадь этого се­че­ния, если бо­ко­вое ребро пи­ра­ми­ды равно а сто­ро­на ос­но­ва­ния равна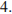

Ответ:

7. C 2 № 500918. В пра­виль­ной тре­уголь­ной пи­ра­ми­де с ос­но­ва­ни­ем сто­ро­на ос­но­ва­ния равна а угол равен На ребре взята точка так, что — бис­сек­три­са угла Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды, про­хо­дя­ще­го через точки и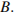

Ответ:

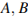8. C 2 № 500962. В пра­виль­ной тре­уголь­ной приз­ме сто­ро­ны ос­но­ва­ния равны 6, бо­ко­вые рёбра равны 4. Изоб­ра­зи­те се­че­ние, про­хо­дя­щее через вер­ши­ны и се­ре­ди­ну ребра Най­ди­те его пло­щадь.

Ответ:

9. C 2 № 500968. В пра­виль­ной тре­уголь­ной приз­ме сто­ро­ны ос­но­ва­ния равны , бо­ко­вые рёбра равны . Изоб­ра­зи­те се­че­ние, про­хо­дя­щее через вер­ши­ны и се­ре­ди­ну ребра 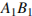. Най­ди­те его пло­щадь.

Ответ: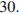

10. C 2 № 501124. В пра­виль­ной тре­уголь­ной приз­ме ABCA'B'C' сто­ро­ны ос­но­ва­ния равны 6, а бо­ко­вые ребра равны 4. Изоб­ра­зи­те се­че­ние, про­хо­дя­щее через вер­ши­ны A, B и се­ре­ди­ну ребра A'C'. Най­ди­те его пло­щадь

Ответ:

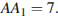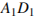11. C 2 № 501710. В пра­виль­ной четырёхуголь­ной при­зме сто­ро­на ос­но­ва­ния равна а бо­ко­вое ребро Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этой приз­мы плос­ко­стью, про­хо­дя­щей через точки и

Ответ:

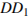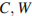12. C 2 № 501752. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и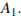

Ответ:

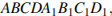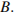13. C 2 № 501885. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра: Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и

Ответ:

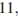14. C 2 № 502294. В пра­виль­ной четырёхуголь­ной приз­ме сто­ро­на ос­но­ва­ния равна а бо­ко­вое ребро 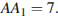Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этой приз­мы плос­ко­стью, про­хо­дя­щей через точки и

Ответ:

15. C 2 № 502314. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру и делит его в от­но­ше­нии 4:5, счи­тая от вер­ши­ны 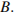Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точк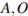и и

Ответ:

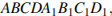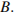16. C 2 № 503147. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра: Точка при­над­ле­жит ребру и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и

Ответ:

17. C 2 № 505417. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC сто­ро­ны ос­но­ва­ния равны 6, а бо­ко­вые рёбра 10. На ребре AC на­хо­дит­ся точка D, на ребре AB на­хо­дит­ся точка E, а на ребре AM — точка L. Из­вест­но, что AD = AE = LM = 4. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L.

Ответ:

18. C 2 № 505423. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC сто­ро­ны ос­но­ва­ния равны 6, а бо­ко­вые рёбра 8. На ребре AC на­хо­дит­ся точка D, на ребре AB на­хо­дит­ся точка E, а на ребре AM — точка L. Из­вест­но, что СD = BE = LM = 2. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L.

Ответ: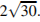

19. C 2 № 505450. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC сто­ро­ны ос­но­ва­ния равны 8, а бо­ко­вые рёбра 16. На ребре AC на­хо­дит­ся точка D, на ребре AB на­хо­дит­ся точка E, а на ребре AM — точка L. Из­вест­но, что CD = BE = LM = 4. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L.

Ответ:

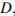20. C 2 № 505471. В тре­уголь­ной пи­ра­ми­де ос­но­ва­ни­ем яв­ля­ет­ся пра­виль­ный тре­уголь­ник ребро пер­пен­ди­ку­ляр­но плос­ко­сти ос­но­ва­ния, сто­ро­ны ос­но­ва­ния равны а ребро На ребре на­хо­дит­ся точка на ребре точка а на ребре — точка Из­вест­но, что и Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки и

Ответ: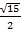

21. C 2 № 505493. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC ребро MB пер­пен­ди­ку­ляр­но плос­ко­сти ос­но­ва­ния, сто­ро­ны ос­но­ва­ния равны 6, а ребро MA равно 11. На ребре AC на­хо­дит­ся точка D, на ребре AB точка E, а на ребре AM — точка F. Из­вест­но, что AD = 4 и BE = 2, F — се­ре­ди­на AM. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и F.

Ответ:

22. C 2 № 505499. В пра­виль­ной тре­уголь­ной пи­ра­ми­де MABC с ос­но­ва­ни­ем ABC ребро MA пер­пен­ди­ку­ляр­но плос­ко­сти ос­но­ва­ния, сто­ро­ны ос­но­ва­ния равны 3, а ребро MB равно 5. На ребре AC на­хо­дит­ся точка D, на ребре AB точка E, а на ребре AM — точка L. Из­вест­но, что AD = 2 и BE = ML = 1. Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точки E, D и L.

Ответ:

 

Дата добавления: 2015-08-17; просмотров: 207 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Срок действия договора| D) Несут все процессуальные обязанности истца.
mybiblioteka.su - 2015-2024 год. (0.01 сек.)