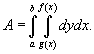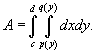Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Площадь плоской фигуры

Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям. | Дифференциалы высших порядков от функции двух аргументов. | Касательная плоскость и нормаль к поверхности в заданной точке. | Скалярное поле, производная по направлению, градиент, их свойства. | Интегрирование тригонометрических функций | Интегрирование дробно-рациональных функций. | Интегрирование некоторых трансцендентных функций. | Интегрирование простейших иррациональных алгебраических функций. | Интегрирование гиперболических функций | Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления) |


Читайте также:
  1. Cравнение отопительных систем среднеутепленного здания площадью 400 м2 (ориентировочно, 2009 год) в зависимости от вида топлива.
  2. Oslash; Площадь боковой поверхности
  3. Б) Найдите площадь сечения.
  4. География, площадь, ландшафт
  5. Геометрические фигуры и их свойства. Измерение геометрических величин.
  6. Дана длина ребра куба. Найти площадь полной поверхности этого куба.
  7. Знать геометрические фигуры: круг, овал, прямоугольник, квадрат, треугольник.

Если f (x,y) = 1 в интеграле , то двойной интеграл равен площади области интегрирования R.

Площадь области типа I (элементарной относительно оси О y) выражается через повторный интеграл в виде

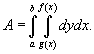
Аналогично, площадь области типа II (элементарной относительно оси О x) описывается формулой

     
     

Дата добавления: 2015-08-20; просмотров: 42 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Площадь поверхности вращения.| Объем тела
mybiblioteka.su - 2015-2024 год. (0.006 сек.)