Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами .

Пример 16. | ВАРИАЦИОННЫЙ РЯД | Выборочное среднее | Доверительный интервал и доверительная вероятность | Два или более случайные величины, описывающих некоторое явление называют системой или комплексом случайных величин. | Построить полигон частот. | По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту. | Тест содержал 25 заданий. Построить гистограмму. | Первый способ | Второй способ |


Читайте также:
  1. B)& В течение 15 дней со дня вручения копии решения, вынесенного судом
  2. B)& До вынесения судом решения по делу
  3. C)& постановление и оглашение решения
  4. G) Решение о восстановлении утраченного судебного решения.
  5. PLM-решения в области автоматизации процессов утилизации изделий.
  6. Quot;Глава 9.1. РЕШЕНИЯ СОБРАНИЙ
  7. U. Его радиоактивность. Изотопы. Распределение в породах. Формы нахождения. U в пегматитовом и гидротермальном процессах

1. Записываем характеристическое уравнение k2 + p ⋅ k + q = 0.

2. Находим корни характеристического уравнения k1 и k2.

3. В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:

o , если ;

o , если ;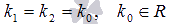

o 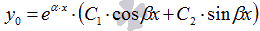, если .

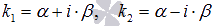Рассмотрим примеры для каждого случая.

Пример.

Найдите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами .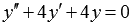

Решение.

Запишем характеристическое уравнение k2 + 4 ⋅ k + 4 = 0. Найдем его корни

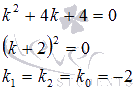
Получили два совпадающих корня, следовательно, общее решение имеет вид .

12.

Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
 
Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: 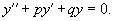Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x) соответствуюшего однородного уравнения и частного решения y 1(x) неоднородного уравнения: 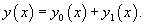Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений. Метод вариации постоянных Если общее решение y 0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: 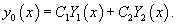Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f (x). Неизвестные функции C 1(x) и C 2(x) определяются из системы двух уравнений: Метод неопределенных коэффициентов Правая часть f (x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
 
  1. где Pn (x) и Qm (x) − многочлены степени n и m, соответственно.
В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Принцип суперпозиции Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
Пример 1
 
Решить дифференциальное уравнение y'' + y = sin(2 x). Решение. Сначала мы решим соответствующее однородное уравнение y'' + y = 0. В данном случае корни характеристического уравнения являтся чисто мнимыми: 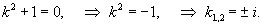Следовательно, общее решение однородного уравнения определяется выражением 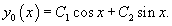Вернемся снова к неоднородному уравнению. Будем искать его решение в виде используя метод вариации постояных. Функции C 1(x) и C 2(x) можно найти из следующей системы уравнений: 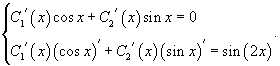Тогда Выразим производную C 1 ' (x) из первого уравнения: 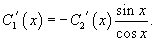Подставляя во второе уравнение, находим производную C 2 ' (x): 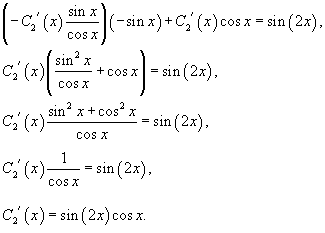Отсюда следует, что 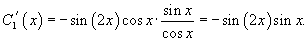Интегрируя выражения для производных C 1 ' (x) и C 2 ' (x), получаем: где A 1, A 2 − постоянные интегрирования. Теперь подставим найденные функции C 1(x) и C 2(x) в формулу для y 1(x) и запишем общее решениенеоднородного уравнения:

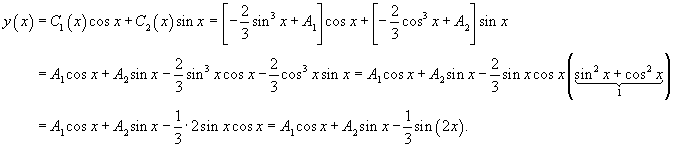
13.ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И НЕЗАВИСИМОСТЬ СИСИТЕМЫ ФУНКЦИЙ НА ОТРЕЗКУ [A,B]

Функции y 1(x), y 2(x),..., yn (x), определённые на отрезке [ a; b ], называются линейно зависимыми на [ a; b ], если существуют постоянные α1, α2,..., α n, не равные нулю одновременно и такие, что α1 y 1(x) + α2 y 2(x) +... + α nyn (x) = 0 для всех x из отрезка [ a; b ].

В противном случае функции y 1(x), y 2(x),..., yn (x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a; b), (a; b ], [ a; b), на бесконечных промежутках.

Справедливо следующее утверждение.

Функции y 1(x), y 2(x),..., yn (x) линейно зависимы на отрезке [ a; b ] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке.

Справедливо следующее утверждение.

Функции y 1(x), y 2(x),..., yn (x) линейно зависимы на отрезке [ a; b ] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других.

Очевидны следующие утверждения.

• Если среди функций y 1(x), y 2(x),..., yn (x) есть нулевая функция, то функции линейно зависимы.

• Если функции y 1(x), y 2(x),..., yk (x) линейно зависимы, то при любых yk + 1(x), yk + 2(x),..., yn (x) функции y 1(x), y 2(x),..., yk (x), yk + 1(x),..., yn (x) также линейно зависимы.

• Если функции y 1(x), y 2(x),..., yn (x) линейно зависимы на отрезке [ a; b ], то они линейно зависимы и на любом отрезке, лежащем внутри [ a; b ].

• Если функции y 1(x), y 2(x),..., yn (x) линейно независимы на [ a; b ], то они линейно независимы и на любом отрезке, содержащем отрезок [а; b ] (если, они определены на этом отрезке).

Вектор–функции Y 1(x), Y 2(x),..., Y n (x),

называются линейно зависимыми на отрезке [ a; b ], если существуют постоянные α1, α2,..., α n, не равные нулю одновременно и такие, что

α1 Y 1(x) + α2 Y 2(x) +... + α n Y n (x) = 0

для всех x из отрезка [ a; b ].

В противном случае функции Y 1(x), Y 2(x),..., Y n (x) называются линейно независимыми.

 

ОПРЕДЕЛИТЕЛЬ ВРОНСКОГО

Определителем Вронского W(x; y 1(x), y 2(x),..., yn (x)) называется определитель, первая строка которого образована функциями y 1(x), y 2(x),..., yn (x) из C n -1[ a, b ], а последующие строки образованы производными от функций предыдущей строки:

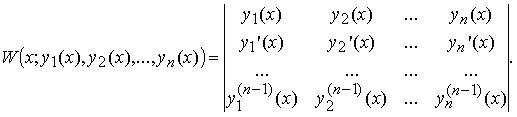
Справедливо следующее необходимое условие линейной зависимости функций.

Если функции y 1(x), y 2(x),..., yn (x) линейно зависимы на отрезке [ a; b ], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y 1(x), y 2(x),..., yn (x)) ≡ 0 на [ a; b ].

Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке.

 

Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Рассмотрим две функции:

Эти функции линейно независимы на [0, 2]. Действительно:

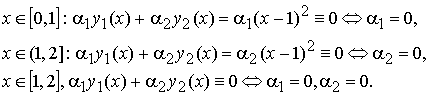
Вычислим определитель Вронского W(x; y 1(x), y 2(x)) на [0, 2]:

Итак, функции линейно независимы на [0, 2], а W(x; y 1(x), y 2(x)) ≡ 0 на [0, 2].

Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций.

С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций.

(Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём).

Определителем Вронского вектор-функций Y 1(x), Y 2(x),..., Y n (x),

называется определитель W [ x; Y 1, Y 2,..., Y n ], заданный равенством

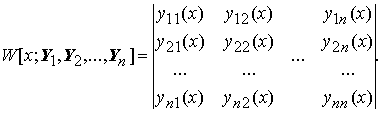
14.СВОЙСТВА РЕШЕНИЙ ЛИНЕЙНОГО ОДНОРОДНОГО УРАВНЕНИЯ N-ГО ПОРЯДКА

Дата добавления: 2015-08-18; просмотров: 141 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.| Свойства линейных однородных дифференциальных уравнений.
mybiblioteka.su - 2015-2024 год. (0.011 сек.)