По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту.

Количество баллов x

Число учащихся n

Решение.

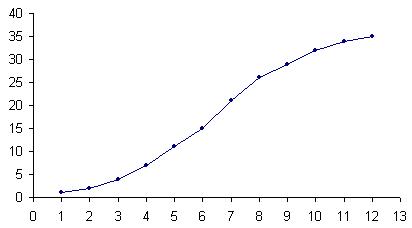
Cоставим кумулятивный вариационный ряд (см. таблицу ниже), для которого построим кумуляту.

Количество баллов

Частота

Накопленная частота n

Гистограмму используют для изображения интервальных рядов. Для построения гистограммы по данным вариационного ряда с равными интервалами, как и для построения полигона, на оси абсцисс откладывают значения аргумента, а на оси ординат - значения частот или относительных частот. Далее строят прямоугольники, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов, а высотами - отрезки, длины которых пропорциональны частотам или относительным частотам соответствующих интервалов.

В результате получают ступенчатую фигуру в виде сдвинутых друг к другу прямоугольников, площади которых пропорциональны частотам (или относительным частотам).

Если интервалы неравные, то на оси ординат следует откладывать в произвольно выбранном масштабе значения плотности распределения (абсолютной или относительной). Таким образом, высоты прямоугольников, которые мы строим, должны равняться плотностям соответствующих интервалов.

При графическом изображении вариационного ряда с помощью гистограммы плотность изображается так, как если бы она оставалась постоянной внутри каждого интервала. На самом деле, как правило, это не так. Если построить распределение по частям интервалов, то можно убедиться в том, что плотность распределения на различных участках интервала не остается постоянной. Плотность, полученная ранее, предствляла лишь некоторую среднюю плотность. Итак, гистограмма изображает не фактическое изменение плотности распределения, а лишь средние плотности распределения на каждом интервале.

Если построена гистограмма интервального распределения, то полигон того же распределения можно получить, если соединить прямолинейными отрезками середины верхних оснований прямоугольников.

Дата добавления: 2015-08-18