
Читайте также:
|
Пусть x и у - случайные величины. Тогда D(x+y)=M[((x+y)-M(x+y))2]= =M[((x-Mx)+(y-My))2]=M[(x-Mx)2+(y-My)2+2*(x-Mx)*(y-My)]=M[(x-Mx)2]+ +M[(y-My)]+2*M[(x-Mx)*(y-My)]=D(x)+D(y)+2*COV(x,y).
Величина COV(x,y)=M[(x-Mx)*(y-My)] называется ковариацией и обладает свойством: ДЛЯ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КОВАРИАЦИЯ ВСЕГДА РАВНА НУЛЮ. Отсюда, следует: ДИСПЕРСИЯ СУММЫ ДВУХ НЕЗАВИСИМЫХ (И ТОЛЬКО НЕЗАВИСИМЫХ) СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН.
11. Локальная и интегральная формулы Муавра-Лапласа
При достаточно большом n и не слишком малых p и q формула Пуассона уже даёт значительную погрешность и применяется другое приближение – формула Муавра - Лапласа, которую можно получить из формулы Бернулли, совершая предельный переход и применяя формулу Стирлинга для вычисления 
 где
где 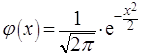 и
и  (1.21)
(1.21)
Эта формула также табулирована (Таблица 3), причём в силу чётности функции  , таблица её значений составлена только для
, таблица её значений составлена только для 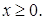
Если при сохранении условий предыдущего пункта нас интересует вероятность того, что при  испытаниях событие
испытаниях событие  появляется не менее
появляется не менее  и не более
и не более 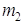 раз, то формула (1.18) с учётом предельного перехода превращается в интегральную формулу Муавра-Лапласа:
раз, то формула (1.18) с учётом предельного перехода превращается в интегральную формулу Муавра-Лапласа:
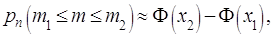
где

и сумма превращается в интеграл. Функция 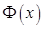 – интеграл от
– интеграл от  – называется функцией Лапласа и представляет собой не выражающийся через элементарные функции интеграл. Поскольку функция Лапласа нечётная (
– называется функцией Лапласа и представляет собой не выражающийся через элементарные функции интеграл. Поскольку функция Лапласа нечётная ( ) и быстро приближается к своему асимптотическому значению 0.5, то таблица её значений (Таблица 4) составлена для
) и быстро приближается к своему асимптотическому значению 0.5, то таблица её значений (Таблица 4) составлена для  . Для больших значений аргумента с большой точностью можно принять
. Для больших значений аргумента с большой точностью можно принять  .
.
Дата добавления: 2015-08-18; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО ЭТОЙ ВЕЛИЧИНЕ. | | | Пример 16. |