Читайте также:
|
Пусть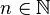 
и 
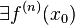. Тогда справедлива формула (1), в которой 
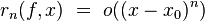при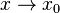 
.
Доказательство: будем проводить по индукции:
При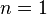 
утверждение теоремы верно. В самом деле, в этом случае 
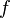дифференцируема в точке 
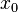. Следовательно,
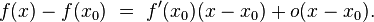
Что совпадает с условием теоремы.
Предположим, что утверждение теоремы верно при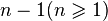 
и покажем, что это верно и для n.
Использую теорему Лагранжа о конечных приращениях и лемму, имеем (считая для определенности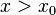 
):
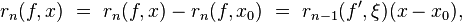
где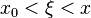 
.
По предположению индукци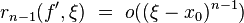и 
при 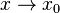. Следовательно,
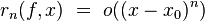при .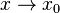
что и требовалось показать.
14.РАЗЛОЖЕНИЕ В РЯД МАКЛОРЕНА e^x, sin(x), cos(x)
Cos(x)=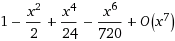 
Sin(x)=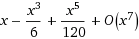 
E^x=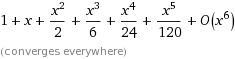 
Дата добавления: 2015-08-18; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема. Формула с остаточным членом в форме Лагранжа. Править | | | Сходимость построенных рядов к соответствующим функциям. |