
|
Читайте также: |
Если a = 0, то такое разложение называется рядом Маклорена:
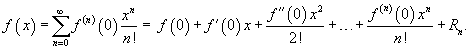 Разложение некоторых функций в ряд Маклорена
Разложение некоторых функций в ряд Маклорена
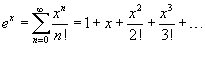
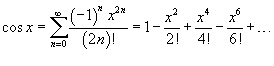
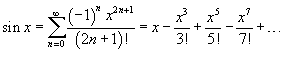


|
| Пример 1 |
Найти ряд Маклорена для функции 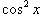 .
Решение.
Воспользуемся тригонометрическим равенством .
Решение.
Воспользуемся тригонометрическим равенством 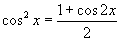 . Поскольку ряд Маклорена для cos x имеет вид . Поскольку ряд Маклорена для cos x имеет вид  , то можно записать , то можно записать
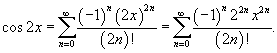 Отсюда следует:
Отсюда следует:
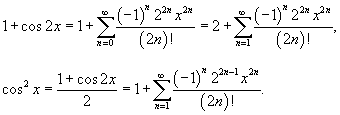
|
13.ОСТАТОЧНЫЙ ЧЛЕН РАЗЛОЖЕНИЯ В РЯД ТЕЙЛОРА В ФОРМЕ ЛАГРАНЖА И ПЕАНО
Дата добавления: 2015-08-18; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула Тейлора | | | Остаточный член формулы Тейлора. |