Сумма бесконечно убывающей геометрической прогрессии

До сих пор, говоря о суммах, мы всегда предполагали, что число слагаемых в этих суммах конечно (например, 2, 15, 1000 и т. д.). Но при решении некоторых задач (особенно высшей математики) приходится сталкиваться и с суммами бесконечного числа слагаемых

S = a ₁ + a ₂ +... + a_n +.... (1)

Что же представляют из себя такие суммы? По определению суммой бесконечного числа слагаемых a ₁, a ₂,..., a_n,... называется предел суммы S _n первых п чисел, когда п —> ∞:

S = 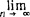S _n = 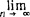(a ₁ + a ₂ +... + a_n). (2)

Предел (2), конечно, может существовать, а может и не существовать. Соответственно этому говорят, что сумма (1) существует или не существует.

Как же выяснить, существует ли сумма (1) в каждом конкретном случае? Общее решение этого вопроса выходит далеко за пределы нашей программы. Однако существует один важный частный случай, который нам предстоит сейчас рассмотреть. Речь будет идти о суммировании членов бесконечно убывающей геометрической прогрессии.

Пусть a ₁ , a ₁ q, a ₁ q ²,...— бесконечно убывающая геометрическая прогрессия. Это означает, что | q |< 1. Сумма первых п членов этой прогрессии равна

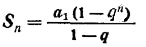
Из основных теорем о пределах переменных величин (см. § 136) получаем:

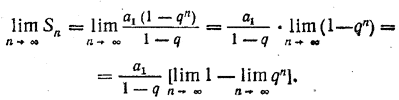
Но 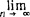1 = 1, a 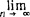qⁿ = 0. Поэтому

Итак, сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрести, деленному на единицу минус знаменатель этой прогрессии.

Примеры.

1) Сумма геометрической прогрессии 1, ¹/₃ , ¹/₉ , ¹/₂₇,... равна

а сумма геометрической прогрессии 12; —6; 3; — ³/₂,... равна

Дата добавления: 2015-08-18