Признак Дирихле

Ряд 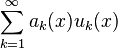сходится равномерно, если выполнены следующие условия:

1. Последовательность действительнозначных функций 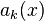монотонна 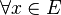и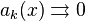

2. Частичные суммы 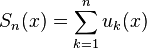равномерно ограничены.

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ часть 2

1. Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда)

2. Числовой ряд – это сумма членов числовой последовательности вида .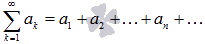

В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: .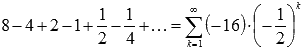

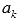называют общим членом числового ряда или k–ым членом ряда.

2.

Исследуем сходимость ряда

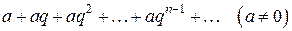, (6)

который называется рядом геометрической прогрессии. Ряд (6) часто используется при исследовании рядов на сходимость.

Как известно, сумма первых n членов прогрессии находится по формуле 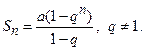Найдем предел этой суммы

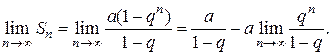
Рассмотрим следующие случаи в зависимости от величины q:

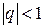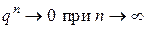1. Если , то . Поэтому 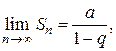ряд (6) сходится, его сумма равна ;

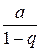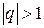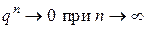2. Если , то . Поэтому 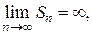ряд (6) расходится;

3. Если 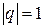, то при 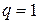ряд (6) принимает вид 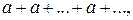для него 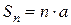и 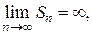т. е. ряд (6) расходится; при 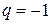ряд (6) принимает вид 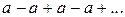– в этом случае 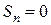при четном n и 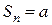при нечетном n. Следовательно, 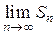не существует, ряд (6) расходится.

Итак, ряд геометрической прогрессии сходится при 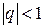и расходится при .

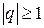Пример 1. Показать, что ряд 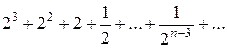сходится.

Решение: Данный ряд можно переписать так:

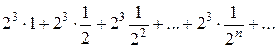
Как видно, он представляет собой ряд геометрической прогрессии с 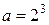и 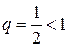. Этот ряд сходится согласно свойству 1 числовых рядов.

Дата добавления: 2015-08-18