Предельные признаки сравнения рядов

Пусть даны два ряда и , у которых члены a_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

· Если 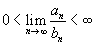, то оба ряда и либо сходятся, либо расходятся;

· Если , то ряд сходится, если сходится ряд ;

· Если , то ряд расходится, если расходится ряд .

Так называемый обобщенный гармонический ряд сходится при p > 1 и расходится при 0 < p ≤ 1.

Определить, сходится или расходится ряд .

Решение.

Воспользуемся признаком сравнения. Заметим, что для всех натуральных n. Ряд 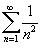является обобщенным гармоническим рядом с p = 2 > 1 и, следовательно, сходится.

Таким образом, исходный ряд сходится по признаку сравнения.

Дата добавления: 2015-08-18