Интервал и радиус сходимости.

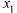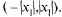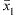Из теоремы Абеля следует, что если — точка сходимости ряда (30.2), то ряд сходится абсолютно во всех точках интервала Если — точка расходимости (30.2), то ряд расходится во всех точках интервалов 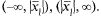Отсюда делаем вывод, что существует такое число R, что на (-R, R) ряд (30.2) сходится абсолютно, а на 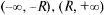расходится. Таким образом, справедлива следующая теорема.

Т: Областью сходимости ряда (30.2) является интервал (-R, R), В каждой точке этого интервала ряд сходится абсолютно, а на интервалах 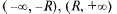— расходится

Интервал (-R, R) называется интервалом сходимости ряда (30.2), a R — его радиусом сходимости. Для некоторых рядов интервал сходимости вырождается в точку (R= 0), для других — охватывает всю ось OX(R= 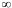). При х= R ряд может и сходиться, и расходиться (вопрос решается для каждого конкретного ряда).

Укажем способ определения радиуса сходимости ряда (30.2). Рассмотрим ряд из абсолютных величин его членов и применим к нему признак Даламбера: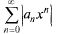

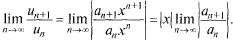
Если 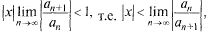то ряд из абсолютных величин членов (30.2) сходится и ряд (30.2) сходится абсолютно. Обозначим

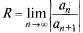(30.4)

При 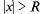ряд (30.2) расходится, так как общий член ряда 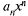не стремится к 0. Таким образом, формула (30.4) дает радиус сходимости.

Пример: Найти радиус и интервал сходимости ряда

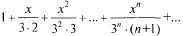
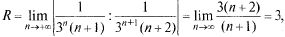
интервал абсолютной сходимости (- 3, 3). На концах интервала: при х = 3 имеем — гармонический расходящийся ряд,

при х= 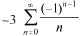— знакочередующийся ряд, сходящийся условно.

Область сходимости данного ряда — промежуток [-3, 3)

Ряд (30.1) сводится к ряду (30.2) заменой переменной 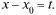Если ряд 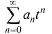имеет радиус сходимости R, то ряд (30.1) сходится абсолютно для 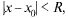т.е. на интервале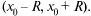

12.РЯДЫ ТЕЙЛОРА

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Определение

Пусть функция 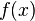бесконечно дифференцируема в некоторой окрестности точки 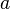. Формальный ряд

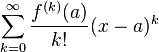
называется рядом Тейлора функции 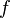в точке .

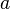То есть, Рядом Тейлора для функции 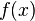в окрестности точки 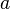называется степенной ряд относительно двучлен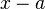а вида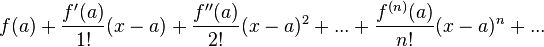

Дата добавления: 2015-08-18