
Читайте также:
|

Гармонический ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:
 .
.
Ряд назван гармоническим, так как складывается из «гармоник»:  -я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной
-я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной  от длины исходной струны.
от длины исходной струны.
5. При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда

существует такое число  ,
,  , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство

то данный ряд абсолютно сходится; если же, начиная с некоторого номера
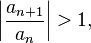
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме[править | править исходный текст]
Если существует предел
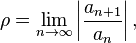
то рассматриваемый ряд абсолютно сходится если  , а если
, а если  — расходится.
— расходится.
Замечание. Если  , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число  , ,  , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство 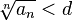 , то данный ряд сходится. , то данный ряд сходится.
|
Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда
 , то
если , то
если 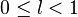 ряд сходится,
если ряд сходится,
если  ряд расходится,
если ряд расходится,
если  вопрос о сходимости ряда остается открытым. вопрос о сходимости ряда остается открытым.
|
6. Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на  , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.
Пусть для функции f(x) выполняется:
1.  (функция принимает неотрицательные значения)
(функция принимает неотрицательные значения)
2.  (функция монотонно убывает)
(функция монотонно убывает)
3.  (соответствие функции ряду)
(соответствие функции ряду)
Тогда ряд  и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
| 7. Абсолютная и условная сходимость рядов | 
| 
| 
|
Дата добавления: 2015-08-18; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сумма бесконечно убывающей геометрической прогрессии | | | Функциональные последовательности |