Читайте также:
|
Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.
Рис.1.10.
Таким образом, интервал 
, за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность - доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.
Доверительный интервал обычно выражают через относительную величину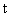 
в долях среднего квадратического отклонения (“кратность”) 
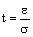. Для нормального закона доверительную вероятность 
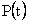определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается 
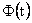и определяется
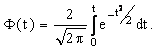
Зная доверительные границы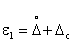 
и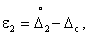 
можно определить доверительную вероятность
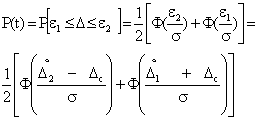
Если значения доверительных границ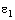 
и 
симметричны, т.е.
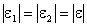, то 
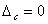и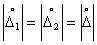 
.
Тогда
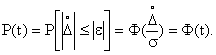
Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности.
Таблица 1.3
| P(t) | 0,90 | 0,95 | 0,99 | 0,999 |
| t | 1,645 | 1,960 | 2,576 | 3,291 |
При нормальном законе распределения доверительный интервал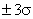 
имеет доверительную вероятность 
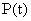=0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше 
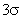. На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение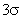 
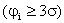, то этот результат считается промахом и исключается из ряда измерений.
Пример. Для известного числа измерений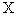 
получены значения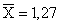 
и 
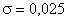. Определить вероятность того, что имеет место неравенство 1,26< 
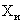<1,28.
Так как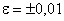 
, то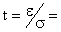 
0,01/0,025=0,4. Используя таблицу интеграла вероятности, находим 
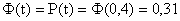. Следовательно, около 30% общего числа измерений будут иметь случайную погрешность 
, не превышающую ±0,01.
17.КОРРЕЛЯЦИОННЫЙ МОМЕНТ.КОЭФФИЦЕНТ КОРРЕЛЯЦИИ.
Корреляционные моменты, коэффициент корреляции
- это числовые характеристики, тесно связанные во введенным выше понятием случайной величины, а точнее с системой случайных величин. Поэтому для введения и определения их значения и роли необходимо пояснить понятие системы случайных величин и некоторые свойства присущие им.
Дата добавления: 2015-08-18; просмотров: 158 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Выборочное среднее | | | Два или более случайные величины, описывающих некоторое явление называют системой или комплексом случайных величин. |