Формула полной вероятности

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Следствием обеих основных теорем – теоремы сложения вероятностей и теоремы умножения вероятностей – является так называемая формула полной вероятности.

Пусть требуется определить вероятность некоторого события , которое может произойти вместе с одним из событий:

,

образующих полную группу несовместных событий. Будем эти события называть гипотезами.

Докажем, что в этом случае

, (3.4.1)

т.е. вероятность события вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Формула (3.4.1) носит название формулы полной вероятности.

Доказательство. Так как гипотезы образуют полную группу, то событие может появиться только в комбинации с какой-либо из этих гипотез:

.

Так как гипотезы несовместны, то и комбинации также несовместны; применяя к ним теорему сложения, получим:

.

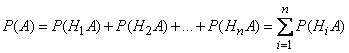Применяя к событию теорему умножения, получим:

,

что и требовалось доказать.

Пример 1. Имеются три одинаковые на вид урны; в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.

Решение. Рассмотрим три гипотезы:

- выбор первой урны,

- выбор второй урны,

- выбор третьей урны

и событие – появление белого шара.

Так как гипотезы, по условию задачи, равновозможные, то

.

Условные вероятности события при этих гипотезах соответственно равны:

.

По формуле полной вероятности

.

Дата добавления: 2015-08-18