Теорема. Формула с остаточным членом в форме Лагранжа. Править

Пусть 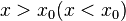, непрерывна на отрезке , на интервале 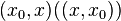. Тогда справедлива формула (1), в которой

где .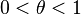

Доказательство: будем проводить по индукции, считая 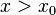. При 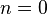теорема утверждает, что при некотором

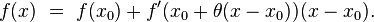
Это утверждение верно, так как оно совпадает с доказанной ранее формулой конечных приращений Лагранжа.

Предположим, что утверждение верно при и установим, что оно верно и при n. Использую теорему Коши о среднем и лемму, имеем (для определенности )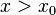

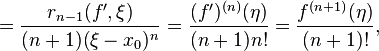
где ,а предпоследнее равенство написано в силу предположения индукции.

Теорема доказана.

О.В Бесов Лекции по математическому анализу.Часть 1. стр.90.

Дата добавления: 2015-08-18