Читайте также:
|
Пусть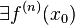 
. Тогда в некоторой окрестности 
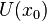можно написать равенство
,
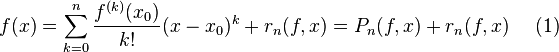которое называется формулой Тейлора функции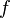 
в точке 
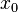, где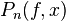 
называется многочленом Тейлора, а 
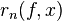- остаточным членом Тейлора (после n-го члена).
Если существует
,
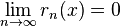то согласно определению сходимости ряда (1) сходится к функции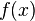 
в точке 
.
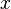Дата добавления: 2015-08-18; просмотров: 81 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| РЯДЫ МАКЛОРЕНА | | | Теорема. Формула с остаточным членом в форме Лагранжа. Править |