Формула бейеса

Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, беря в расчет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятности, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для ее практического применения требуется большое количество расчетов, вычислений, поэтому байесовские оценки стали активно использовать

Пусть событие 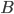происходит одновременно с одним из 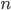несовместных событий 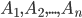. Требуется найти вероятность события 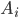, если известно, что событие 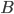произошло.

На основании теоремы о вероятности произведения двух событий можно написать

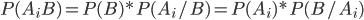
Откуда

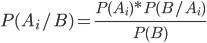
или

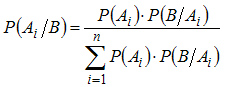(3.2)

Формула (3.2) носит название формулы Байеса.

Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.

Решение. Пусть 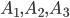— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут

, ,

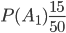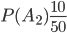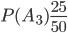
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

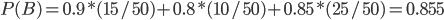
По формуле Байеса находим исходную вероятность

.

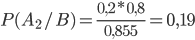8.СХЕМА БЕРНУЛЛИ.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P (A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;

2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Проводятся 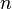опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью 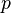(или не произойти — «неудача» — 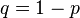). Задача — найти вероятность получения ровно 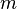успЕхов в опыте.

Решение:

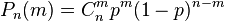
Количество успехов — величина случайная, которая имеет биномиальное распределение.

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

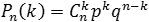
где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача

Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

Решение

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

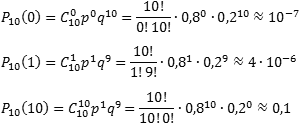
Ответ

10⁻⁷; 4 · 10⁻⁶; 0,1

МАКСИМАЛЬНОЕ ЧИСЛО УСПЕХОВ

Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов 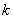(появлений события) имеет вид:

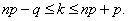
Так как 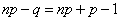, то эти границы отличаются на 1. Поэтому 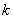, являющееся целым числом, может принимать либо одно значение, когда 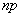целое число (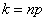), то есть когда 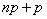(а отсюда и 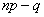) нецелое число, либо два значения, когда 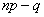целое число.

Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.

Решение. Здесь 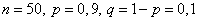. Поэтому имеем неравенства:

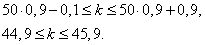
Следовательно, .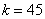

9.АСИМПТОТИЧЕСКАЯ ФОРМУЛА ПУАССОНА

Дата добавления: 2015-08-18