Сходимость построенных рядов к соответствующим функциям.

1. y = e^x.

Имеем f(x) = f'(x) = f''(x) =…= f⁽ⁿ⁾(x) = e^x;

f(0) = f'(0) = f''(0) =…= f⁽ⁿ⁾(0) = e⁰ = 1.

По формуле

e^x = 1 + х + .

Область сходимости ряда (-∞; ∞).

2. y = sin x.

Имеем f(x) = sin x, f'(x) = cos x, f''(x) = -sin x; f'''(x) = -cos x, f⁽⁴⁾(x) = sin x,

откуда f(0) = 0; f'(0) = 1; f''(0) = 0; f'''(0) = -1, f⁽⁴⁾(0) = 0 и т.д.

Очевидно, что производные чётного порядка f⁽²ⁿ⁾(0) = 0, а нечётного порядка f^(2n-1)(0) = (-1)^n-1, i = 1, 2…. По формуле

sin x = x - .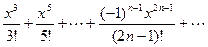

Область сходимости ряда (-∞; ∞).

3. y = cos x.

Рассматривая аналогично, получим

сos x = 1 - .

Область сходимости ряда (-∞; ∞).

15.РАЗЛОЖЕНИЕ В РЯД МАКЛОРЕНА ФУНКЦИЙ ln(1+x);(1+x)^a

ln(1+x)=

Рассмотрим геометрический ряд

= 1 - x + x² - x³ +…+(-1)ⁿ xⁿ +…

со знаменателем q = -х, который сходится при | q | = | -x |<1, т.е. при -1 < х < 1, к функции

.

Интегрируя почленно равенство в интервале (0; х), где | x |<1, с учётом того, что

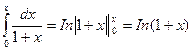, получим

In (1+x) = x - .

Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть .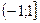

(1+x)^a=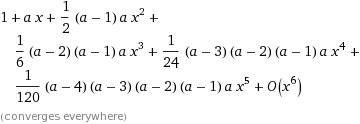

16. РАЗЛОЖЕНИЕ В РЯД МАКЛОРЕНА ФУНКЦИИ arctg(x)

Arctg(x)=

Формула для ряда такая:

arctg x = x −1/3 x 3+1/5 x 5−1/7 x 7+⋯

При x =1/4 он сходится. Рассмотрим приближение

arctg x ≈ x −1/3 x 3

и оценим его точность. Поскольку ряд знакочередующийся, и его члены убывают, для остаточного члена ряда справедливы неравенства

0<1/5 x 5−1/7 x 7+⋯<1/5 x 5=1/5120

при x =1/4. Эта величина меньше δ =10−3, поэтому arctg1/4≈1/4−1/3⋅4^3=47/192≈0,2447916667.... Для сравнения, точное значение равно 0,2449786631....

Дата добавления: 2015-08-18