Читайте также:
|
Рассмотрим ситуацию, в которой число испытаний 
в схеме Бернулли неограниченно увеличивается, а вероятность наступления события 
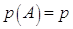в каждом испытании стремится к нулю таким образом, что произведение 
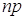остаётся величиной постоянной, которую обозначим 
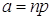. В этом случае имеет место соотношение:
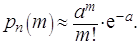(1.19)
Доказательство. По формуле Бернулли
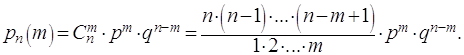
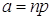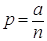Воспользуемся тем, что по условию или 
и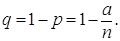 
Формула Бернулли принимает вид:
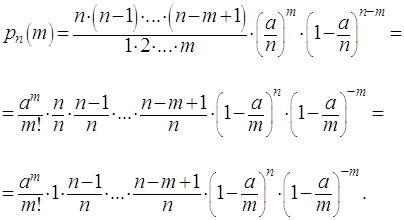
Так как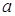 
и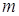 
фиксированы, а стремится к бесконечности, то множител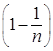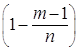и 
; …; 
и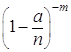 
стремятся к единице, а множитель 
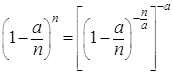стремится к 
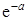, то
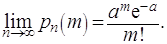
Полученное выражение называется Пуассоновским приближением формулы Бернулли. Эта формула даёт хорошее приближение при достаточно большом и малом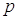 
(например, 
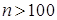и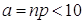 
).
Вероятность события, заключающегося в том, что 
появится не более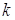 
раз, очевидно, вычисляется по формуле
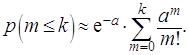(1.20)
При проведении расчётов можно пользоваться тем, что обе формулы табулированы (Таблицы 1 и 2)
10.СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Дата добавления: 2015-08-18; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ФОРМУЛА БЕЙЕСА | | | МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО ЭТОЙ ВЕЛИЧИНЕ. |