Сочетания и их свойства.

Сочетание из n по k, как и размещение, является выборкой k элементов некоего множества, имеющего n элементов, но при этом выборки, отличающиеся порядком и одинаковые по составу, не считаются различными. Напомним, что в случае размещений такие выборки считались бы разными.

Допустим, есть множество {x, y, z}. Сочетаниями по два будут {x, y}, {x, z}, {y, z}.

Количество возможных сочетаний определяется как

Одним из самых любопытных свойств сочетаний является вот такая формула

Если разобраться, то левая часть формулы - количество всевозможных выборок из n элементов без учёта порядка. Рассуждаем. Первый элемент мы можем выбрать либо не выбрать - 2 варианта. Аналогично второй элемент - выбираем либо не выбираем. Так же и с прочими элементами... В итоге получаем произведение n двоек.

Сочетания являются коэффициентами, появляющимися при разложении бинома Ньютона:

Например, при n =3 получим широко известную формулу для куба суммы, как выясняется, частный случай бинома Ньютона:

Теперь ещё раз взгляните на формулу для вычисления количества сочетаний. Из того, что в знаменателе находится k!(n-k)!, а числитель не зависит от k, получаем ещё одно интересное свойство:

Наконец, получим рекуррентное соотношение для расчёта числа сочетаний:

Формулу (*) и полученное рекуррентное соотношение можно скомбинировать:

Это позволит ускорить вычисление коэффициентов разложения бинома Ньютона в сравнении с использованием первой версии рекуррентного соотношения, поскольку теперь почти половину величин не нужно находить по-честному. Примечание: [ x ] - целая часть числа x, для положительных чисел это по сути отсечение дробной части (или отсутствие изменений, если дробной части нет).

ТРЕУГОЛЬНИК ПАСКАЛЯ

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Имеет применение в теории вероятностей.

Свойства

Числа треугольника симметричны (равны) относительно вертикальной оси.

· В строке с номером n:

· первое и последнее числа равны 1.

· второе и предпоследнее числа равны n.

· третье число равно треугольному числу 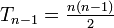, что также равно сумме номеров предшествующих строк.

· четвёртое число является тетраэдрическим.

· m -е число (при нумерации с 0) равно биномиальному коэффициенту .

· Сумма чисел восходящей диагонали, начинающейся с первого элемента (n -1)-й строки, есть n -е число Фибоначчи:

· Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.

· Сумма чисел n -й строки треугольника Паскаля равна .

· Все числа в n -й строке, кроме единиц, делятся на число n, если и только если n является простым числом^[3] (следствие теоремы Люка).

· Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3 n, 3 n +1, 3 n +2, то первые две суммы будут равны, а третья на 1 меньше.

· Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.

6. УСЛОВНАЯ ВЕРОЯТНОСТЬ

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет
.
Вероятность события А при условии, что событие В не произошло, будет
.

Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Решение. Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А - появление первой карты такой масти, В - появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому придется воспользоваться теоремой умножения в ее общей форме:

,
где (после вынимания первой карты осталось 35 карт, из них той же масти, что и первая - 8).

Получаем
.

События, состоящие в том, что будут вынуты две карты масти «пики», масти «треф» и т.д., несовместны друг с другом. Следовательно, для нахождения вероятности их объединения воспользуемся теоремой сложения:
.

Дата добавления: 2015-08-18