Читайте также:
|
Нехай многочлен
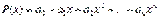
потрібно розвинути за степенями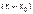 
, де 
– де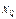яке число, тобто многочлен необхідно записати у вигляді
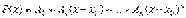, (1)
де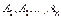 
– невідомі коефіцієнти. Приймаючи 
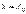, в останній рівності, одержимо 
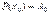. Обчислюючи похідні 
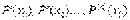, знайдемо послідовно всі коефіцієнти 
:
.
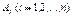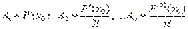Підставляючи коефіцієнти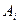 
в розклад (1), отримаємо формулу Тейлора для многочлена:
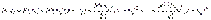
Формулу Тейлора можна записати для довільної функції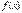 
, яка диференційована 
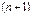разів включно в околі точки 
:
.
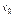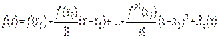Як бачимо, у формулі Тейлора для довільної функції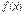 
, крім тейлорівського многочлена 
степеня 
, наявний доданок 
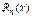, який називають залишковим членом. Залишковий член у формі Лагранжа має вигляд
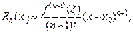
де точка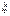 
розміщенa між точками 
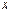і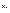 
. Очевидно, що для многочленів 
.
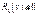Формула Тейлора, якщо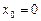 
, називається формулою Маклорена:
.
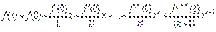59. Означення монотонності. Необхідна та достатня умови монотонності функції.
Моното́нна фу́нкція — це функція, приріст якої не змінює знаку, тобто завжди або невід’ємний, або недодатній. Якщо при цьому приріст ще і не дорівнює нулю, то функція називається стро́го моното́нною.
Дата добавления: 2015-08-17; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Має вигляд | | | Поняття локального екстремуму функції. Наслідок теореми Ферма. |