Має вигляд

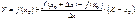
де X і Y – змінні координати точки січної. Кутовий коефіцієнт січної 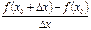при 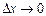прямує до 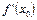. А тому граничне положення січної визначається рівнянням

.

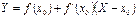Пряма, яка задається цим рівнянням, називається дотичною до графіка функції 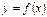у точці 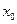. Кутовий коефіцієнт дотичної .

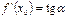Остання формула приводить до геометричного змісту похідної: похідна 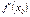функції 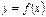у точці 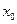дорівнює кутовому коефіцієнту дотичної до графіка функції 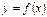, проведеної в точці .

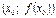Геометричне тлумачення похідної як кутового коефіцієнта дотичної до графіка функції поширюється і на випадок нескінченної похідної. У цьому разі дотична паралельна осі Оу.

2.2. Задача про миттєву швидкість

Розглянемо нерівномірний прямолінійний рух тіла, що розпочинається в момент часу 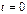. Вважатимемо, що шлях, подоланий тілом за час 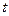, дорівнює 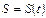. Функція 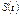називається законом руху тіла.

Шлях 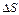, який подолає тіло за відрізок часу 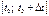, знаходиться як

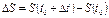
Середньою швидкістю 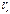руху за проміжок часу 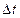називається відношення

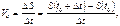
в якому легко пізнати диференціальне відношення.

Миттєвою швидкістю руху 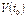в момент 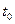називається границя цього відношення, якщо 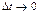, тобто

.

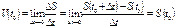Отже, похідна від шляху за часом дорівнює миттєвій швидкості прямолінійного руху тіла.

2.3. Задачі про витрати виробництва та виручку

Нехай 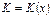- витрати виробництва однорідної продукції – деяка функція кількості продукції х. Зазначимо, що кількості продукції 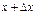відповідають витрати виробництва продукції 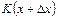. Отже, диференціальне відношення, що характеризує середній приріст витрат виробництва,

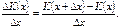
Воно відбиває приріст витрат виробництва на одиницю приросту кількості продукції.

Границя

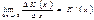
називається граничними витратами виробництва.

Нехай 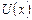- виручка від продажу х одиниць товару. Міркування, аналогічні до попередніх, приводять до границі

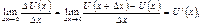
яку називають граничною виручкою.

Похідні основних елементарних функцій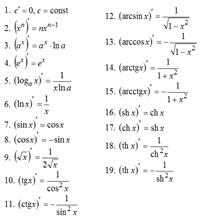

47. Диференційованість функції в точці Нехай функція 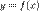визначена в деякому околі точки 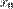і нехай 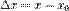. Функція 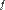називається диференційовною в точці, якщо приріст 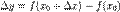можна представити у вигляді:

.

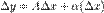де:

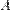— стала. При фіксованій 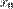A не залежить від 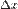; але, при зміні 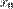, взагалі кажучи, A також змінюється,

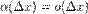при .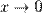

Лінійна функція 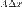(від 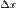) називається диференціалом функції в точці 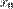і позначається 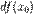, або, коротше .

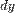Таким чином:

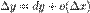при ,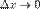

.

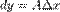Властивості

Для того, аби функція 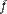була диференційовна в деякій точці 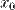, необхідно і достатньо щоб вона мала похідну в цій точці, при чому, в цьому випадку:

.

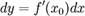Якщо функція диференційовна в деякій точці, то вона також є неперервною в цій точці.

48. Диференціал функції. Нехай функція 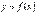має в даній точці 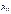скінченну похідну 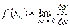. Тоді 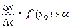, де 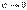, якщо . Звідки

.

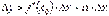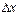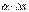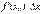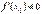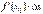Якщо - нескінченно малий приріст, то доданок є нескінченно малим вищого порядку, ніж доданок і якщо , то і 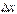-нескінченно малі одного порядку.

Означення. Якщо функція 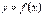має похідну 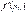в точці 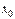, то вираз 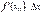називається диференціалом функції в цій точці і позначається символом 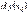. Тобто,

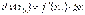
Зауваження. Диференціал функції 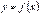в даній точці є головною лінійною частиною приросту функції, пропорційною приросту аргументу з коефіцієнтом пропорційності :

.

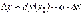Диференціал незалежної змінної ототожнюється з її приростом, тобто

.

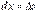Для будь-якої диференційовної в точці х функції 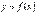формулу можна записати так:

.

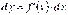Звідки отримаємо, що ,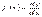

тобто похідну можна розглядати як відношення двох диференціалів.

Правила знаходження диференціала

З правил знаходження похідної випливають правила знаходження диференціала. Якщо функції 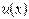, 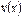-диференційовні в точці х, то

1) .

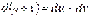2)

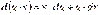
Зауваження. 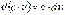, де .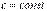

3) , .

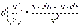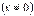Застосування диференціала в наближених обчисленнях

З означення похідної функції в точці 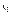випливає, що її приріст можна подати у вигляді: 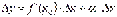, де 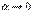, якщо .

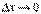Отже, при малих 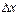має місце наближена рівність:

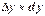, тобто .

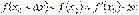Звідки .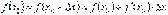

Ця формула дозволяє знаходити значення функції 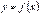в точці 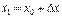, якщо відомі значення 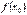і 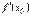, з точністю ,

де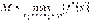

49. Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оборотною.
У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.
Інакше кажучи, якщо функція 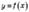є оборотною й число а належить до її області значень 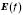, то рівняння 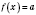має розв’язок, причому єдиний.
Оберненою до даної оборотної функції 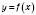називається така функція 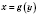, яка кожному із множини значень функції 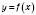ставить у відповідність єдине число x з області визначення.
Якщо аргумент і функцію в записі 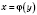позначити звичайним способом, отримаємо .
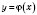Графік функції g, оберненої до функції f, симетричний графіку f відносно прямої .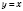
Якщо функція f зростає (або спадає) на проміжку I, то вона є оборотною. Обернена до f функція g, яка визначена в області значень f, теж є зростаючою (або спадною).
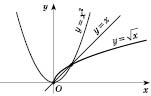
Наприклад: На проміжку 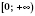функція 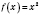є оборотною. Оберненою до неї на цьому проміжку є функція .
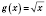На рисунку зображені функція і обернена до неї функція :

Похідна оберненої функції.

Теорема Якщо функція 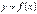, , 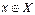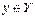має обернену 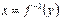і для всіх 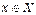існує похідна 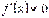, то для всіх 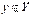існує похідна 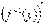, причому справедлива рівність:

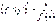або , .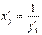

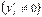Доведення. З означення похідної маємо:

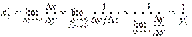, тобто , .

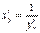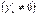50. Зв’язок диференційованості з неперервністю

Теорема (про зв’язок між поняттями диференційованості і неперервності). Якщо функція 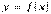диференційована в точці 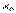, то вона в цій точці неперервна
Доведення. Оскільки функція 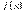диференційована в точці 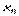, то існує границя

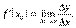
Запишемо тотожність

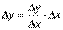
і перейдемо в ній до границі, якщо 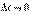. Отримаємо

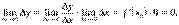
А це й означає, що функція 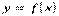неперервна в точці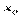
Підкреслимо, що функція 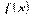неперервна в точці 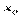, не обов’язково диференційована в цій точці. Так, наприклад, функція 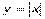, про яку йшлося вище, очевидно, неперервна в точці 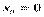, проте похідної в цій точці немає.

52. Похідні та диференціали вищих порядків

Нехай функція 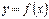диференційовна на проміжку X, а 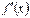- її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної називається похідною другого порядку функції 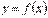і позначається одним із символів:

.

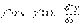Так у фізиці, якщо 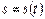- закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то 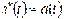є прискоренням цієї точки в момент часу t.

Аналогічно 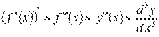і т. д.

Взагалі похідною n-го порядку від функції 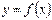називається похідна від похідної 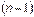-го порядку і позначається

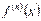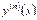, або , або .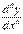

Зауваження. При 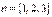, похідну n-го порядку позначають відповідно 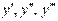; при 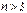позначають: 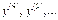або .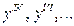

Теорема Лейбніца. Якщо функції 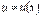, 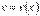мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:

диференціал

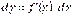
називається також диференціалом першого порядку і його можна розглядати як функцію змінної x(приріст аргументу 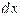вважається сталим).

Означення: Диференціалом другого порядку (second differential) функції 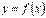в точці xназивається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім 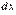) і позначається :

.

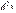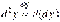За означенням маємо

,

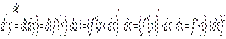позначають 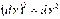. Таким чином

.

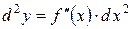Аналогічно, диференціалом n-го порядку (позначається 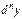), n=2,3,... називається диференціал від диференціала порядку 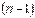за умови, що в диференціалах весь час беруться одні й ті самі прирости 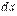незалежної змінної x. Тобто

.

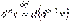При цьому справедлива формула:

.

.

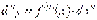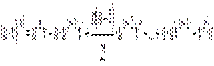53.Теорема Ролля: Нехай функція 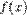неперервна на проміжку 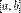, диференційована в усіх внутрішніх точках проміжку 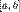. Нехай, окрім того, 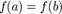. Тоді на проміжку 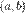знайдеться принаймні одна точка така, що значення похідної у цій точці 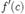дорівнює нулю.

Доведення:

Оскільки функція 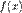неперервна на проміжку 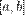, то, згідно з другою теоремою Вейєрштрасса, ця функція досягає на ньому свого максимального значення та мінімального значення 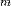. Отже, маємо два випадки:

1. ;

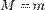2. ;

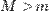В першому випадку 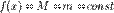. Тому похідна 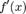дорівнює нулю в будь-якій точці проміжка .

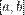У випадку, коли 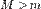, оскільки 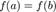, можна стверджувати, що хоча б одне з двох значень 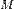чи 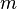досягається функцією в деякій внутрішній точці проміжка 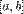. Але тоді функція 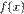має у точці локальний екстремум. Оскільки функція 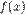диференційовна в точці , то за необхідною умовою локального екстремуму, .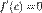

54. Теорема Лагранжа:

Теорема. Якщо функція 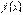: 1) задана і неперервна на відрізку ; 2) диференційована в інтервалі , то тоді всередині інтервалу 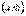знайдеться хоча б одна точка 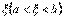, в якій справджуються рівність

.

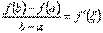Д о в е д е н н я. Розглянемо функцію ,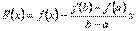

що задовольняє всім умовам теореми Ролля. Справді, 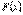на відрізку є неперервною (як різниця двох неперервних функцій), а всередині інтервалу має похідну

;

.

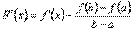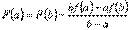Отже, існує точка 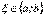в якій 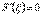або, що саме,

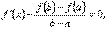
звідси

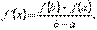
Теорему доведено.

55. Теорема Коші (про відношення приростів двох функцій)

Теорема: Якщо функці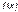ї і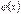

1) неперервні на відрізку, ,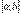

2) диференційовні в інтервалі (a,b) , причому 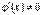,то в цьому інтервалі існує точка 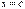, 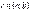така, що має місце рівність:

.

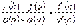Доведення. Рівність (1) можлива, оскільки , .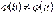

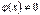
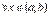Побудуємо допоміжну функцію 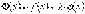, де 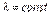. Підберемо 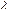так, щоб функція 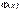на кінцях відрізка мала рівні значення :

, .

.

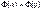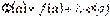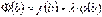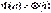
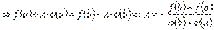Тоді

.

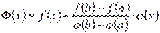Функція 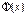задовольняє умови теореми Ролля. Отже за цією теоремою знайдеться таке 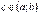, що .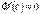

Знайдемо похідну 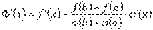. Тоді з умови 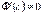матимемо, що 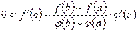, звідки

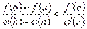, що і потрібно було довести.

Зауваження. Якщо в рівності 1 прийняти 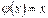, то як наслідок отримаємо теорему Лагранжа.

56. Правила Лопіталя. І правило Лопіталя). Якщо: 1) функції і 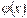диференційовні на інтервалі 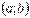, 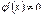для всіх ;

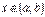2) ;

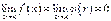3) існує скінченна або нескінченна границя ,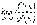

то існує границя 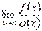, причому має місце рівність: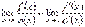

.

Доведення. Довизначимо функці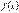ї і 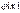в точці 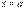так, щоб вони стали неперервними, тобто покладемо 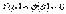. Тепер 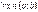ці функції на відрізку 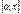, (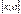) задовольняють умови теореми Коші. Тому існує точка с, 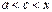, (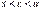) така, що .

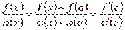Оскільки 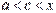, (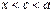) то 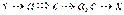. Перейшовши в останній рівності до границі, за умови 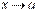, отримаємо

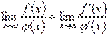що і потрібно було довести.

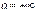Наслідок 1. Теорема Лопіталя справедлива також при , при і при .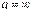

Наслідок 2. Якщо похідн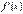і і 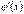задовольняють ті самі вимоги, що і функці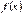ї і 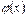, то правило Лопіталя можна застосувати повторно. При цьому отримаємо

.

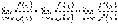І взагалі, правило Лопіталя при виконанні умов теореми можна застосовувати багаторазово.

Наслідок 3. Якщо в теоремі замінити умову 2) на наведену нижче

2) 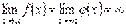, або 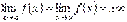, то формула (3.21) також має місце.

В цьому випадку правило Лопіталя застосовується для розкриття невизначеності типу 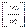(ІІ правило Лопіталя).

57. Асимптоти графіка функції Пряма називається асимптотою кривої, якщо точка кривої необмежено наближається до неї при зростанні абсциси чи ординати. Асимптоти поділяють на вертикальні, похилі (горизонтальні) асимптоти.

ВЕРТИКАЛЬНІ АСИМПТОТИ

Графік функції при має вертикальну асимптоту,якщо границя функції нескінченна

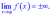
Крім цьому точка 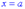є точкою розриву II роду, а рівняння вертикальної асимптоти має вигляд

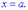
ПОХИЛІ АСИМПТОТИ

Рівняння похилої асимптоти має вигляд

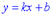
де 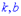- границі, що обчислюються за правилом

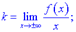
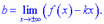
Якщо обидві границі існують і скінченні то функція має похилу асимптоту, інакше – не має. Слід окремо розглядати випадки, коли та .

ГОРИЗОНТАЛЬНІ АСИМПТОТИ

Крива 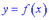має горизонтальну асимптоту тільки в тому випадку, коли існує скінченна границя функції при та , і ця границя рівна

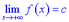
або

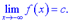
Знаходження границь в деяких випадках спрощується, якщо застосовувати правило Лопіталя.

Дата добавления: 2015-08-17