Поняття локального екстремуму функції. Наслідок теореми Ферма.

Точка називається точкою локального мінімуму або максимуму функції 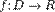, якщо 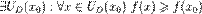для точки мінімуму, або для точки максимуму. Якщо знак нерівності строгий, то отримаємо строгий локальний мінімум або максимум.

Екстремум — найбільше та найменше значення функції на заданій множині.

Розрізняють:

· локальний — екстремум в деякому довільно малому околі даної точки

· глобальний — екстремум в усій розглядуваній області значень функцій

Необхідна умови існування екстремуму функції: Якщо функція має в точці локальний екстремум, то або , або не існує.

Точки, які задовольняють виписаним вище вимогам ще називають критичними точками.

Доведення: Нехай у точці функція f(x) має локальний екстремум, але тоді ) ⇨

Для ∆x >0

Для ∆x 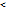0

Переходячи до границі при 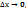отримаємо 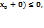f’( f’( а тому, або не існує f’, або якщо

61. І достатня умова існування локального екстремуму. Теорема І. Нехай функція 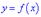неперервна в деякому інтервалі, що містить критичну точку , і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки ).

Тоді для точки функція має максимум, якщо для аргументів виконується 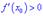, а для 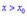умова .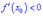

Якщо ж для похідна менша нуля 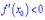, а для більша нуля 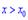, то для точки 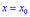функція має мінімум.

Дата добавления: 2015-08-17