Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

ІІ достатня умова існування локального екстремуму.

До поняття похідної приводять різноманітні задачі геометрії, механіки, хімії, економіки, біології та інших наук. Розглянемо деякі з них. | Має вигляд | Формули Тейлора і Маклорена |


Читайте также:
  1. Використання результатів бонітування ґрунтів та економічної оцінки земель в сучасних умовах.
  2. Влияние на организм производственного шума. Шумовая болезнь. Меры профилактики.
  3. Економічний націоналізм – стратегія захисту національних економік в умовах глобалізації.
  4. Заведующий кафедрой __________________Е.А. Авакумова
  5. Інноваційні, інформаційно-технологічні, фінансово-економічні, інституціональні й соціальні засади трансформації світових економічних стратегій в умовах глобалізації.
  6. Концептуальні основи трансформації міжнародних економічних стратегій в умовах глобалізації.

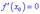Теорема ІІ. Нехай функція два рази диференційована в околі точки і похідна рівна нулю . Тоді в точці 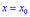функція має локальний максимум, якщо друга похідна менша нуля , і локальний мінімум, якщо навпаки .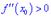

Якщо ж , то точка 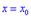може й не бути точкою екстремуму.

Дата добавления: 2015-08-17; просмотров: 60 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Поняття локального екстремуму функції. Наслідок теореми Ферма.| Опуклість і вгнутість графіка функції. Точки перегину
mybiblioteka.su - 2015-2024 год. (0.007 сек.)