
Читайте также:
|
Заменим
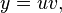
тогда:
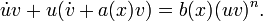
Подберем 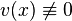 так, чтобы было
так, чтобы было
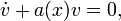
для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения 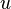 получаем уравнение
получаем уравнение 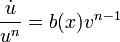 — уравнение с разделяющимися переменными.
— уравнение с разделяющимися переменными.
Пример
Уравнение
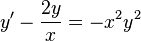
разделим на 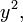 получаем:
получаем:
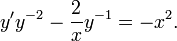
Замена переменных
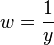
дает:
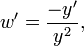
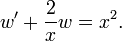
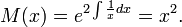
Делим на 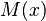 ,
,
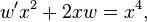
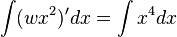
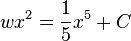
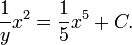
Результат:
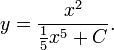
7.ОСОБЫЕ РЕШЕНИЯ ДУ 1-ГО ПОРЯДКА
Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример: Рассмотрим дифференциальное уравнение:
y = 3(y − sin x) + cos x. (1)
Непосредственной проверкой нетрудно убедиться, что при любом С функция
y = (x + C) + sin x (2)
есть решение этого уравнения. Здесь семейство интегральных кривыхзадается с помощью функции
Ф(x, y,C) = y − (x + C) − sin x.
Для нахождения уравнения огибающей имеем систему
Ф(x, y,C) = y − (x + C) − sin x = 0
Ф (x, y,C) = −3(x + C) = 0
Отсюда x + C = 0, и y = sin x. Надо еще проверить, что последнее равенство задает огибающую.
Легко видеь, что при х=х кривые y = sin x и y = (x − x0)3 + sin x имеют общую в точке с абциссой
x = x. Поэтому y = sin x – огибающая семейства кривых (2) и, следовательно,
особое решение уравнения (1).
9.ДУ 2-ГО ПОРЯДКА
| Дифференциальные уравнения второго порядка |
| 1. Основные понятия |
Дифференциальное уравнение второго порядка можно записать в виде 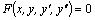 . Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде . Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде
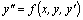 .
Для этих уравнений имеет место теорема существования и единственности решения.
Теорема. Если в уравнении .
Для этих уравнений имеет место теорема существования и единственности решения.
Теорема. Если в уравнении 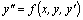 функция функция  и ее частные производные по аргументам y и и ее частные производные по аргументам y и 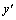 непрерывны в некоторой области, содержащей непрерывны в некоторой области, содержащей 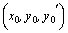 , то существует и притом единственное решение , то существует и притом единственное решение 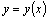 уравнения, удовлетворяющее условиям уравнения, удовлетворяющее условиям 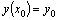 и и 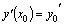 .
Эти условия называются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости .
Эти условия называются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости 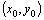 с заданным тангенсом угла наклона касательной с заданным тангенсом угла наклона касательной 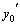 проходит единственная интегральная кривая. Ясно, что если мы будем задавать различные значения проходит единственная интегральная кривая. Ясно, что если мы будем задавать различные значения 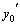 , то при постоянных , то при постоянных 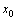 и и 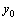 мы получим бесчисленное множество интегральных кривых с различными углами наклона касательных и проходящих через заданную точку.
Общим решением дифференциального уравнения второго порядка называется функция мы получим бесчисленное множество интегральных кривых с различными углами наклона касательных и проходящих через заданную точку.
Общим решением дифференциального уравнения второго порядка называется функция 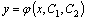 , зависящая от двух произвольных постоянных, которая при любых значениях , зависящая от двух произвольных постоянных, которая при любых значениях 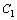 и и 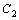 является решением дифференциального уравнения.
Уравнение является решением дифференциального уравнения.
Уравнение  , определяющее общее решение, называется общим интегралом дифференциального уравнения.
Если в общее решение подставить конкретные значения , определяющее общее решение, называется общим интегралом дифференциального уравнения.
Если в общее решение подставить конкретные значения 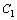 и и 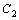 , то получится частное решение дифференциального уравнения. График частного решения называют интегральной кривой данного дифференциального уравнения.
Рассмотрим методы решения некоторых уравнений второго порядка. , то получится частное решение дифференциального уравнения. График частного решения называют интегральной кривой данного дифференциального уравнения.
Рассмотрим методы решения некоторых уравнений второго порядка.
|
| 2. Уравнения, допускающие понижение порядка |
а) Рассмотрим простейшее уравнение второго порядка 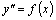 . Общее решение такого уравнения получается путем двукратного интегрирования: . Общее решение такого уравнения получается путем двукратного интегрирования:
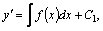
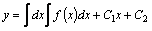 ,
где ,
где 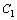 и и 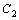 –произвольные постоянные, а неопределенные интегралы трактуются как первообразные соответствующих функций.
Пример 7. Решить уравнение –произвольные постоянные, а неопределенные интегралы трактуются как первообразные соответствующих функций.
Пример 7. Решить уравнение 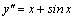 .
Решение. Интегрируя первый раз, получаем .
Решение. Интегрируя первый раз, получаем 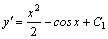 . Общее решение данного уравнения получаем, интегрируя второй раз: . Общее решение данного уравнения получаем, интегрируя второй раз: 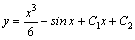 .
б) Рассмотрим уравнение .
б) Рассмотрим уравнение 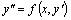 , явно не содержащее искомую функцию y. Положим , явно не содержащее искомую функцию y. Положим 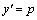 . Тогда . Тогда 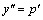 и уравнение примет вид и уравнение примет вид 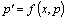 .
Решаем теперь это уравнение первого порядка относительно p, а затем заменяем p на .
Решаем теперь это уравнение первого порядка относительно p, а затем заменяем p на 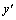 и решаем последнее уравнение относительно неизвестной функции y. и решаем последнее уравнение относительно неизвестной функции y.
|
| Общее и частное решения уравнения высшего порядка | 
| 
| 
|
Дата добавления: 2015-08-18; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Первый способ | | | Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. |