Читайте также:
|
3.1. Если ряд 
сходится, то его общий член стремится к нулю при неограниченном возрастании 
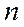, т.е. 
.
3.2. Если 
-й член ряда не стремится к нулю при 
, то ряд расходится.
Примечание: Рассмотренный признак является только необходимым, но не является достаточным, т.е. из того, что 
-й член ряда стремится к нулю, ещё не следует, что ряд сходится, - ряд может и расходится.
Например, так называемый гармонический ряд 
Расходится, хотя 
Дата добавления: 2015-07-25; просмотров: 32 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства сходящихся числовых рядов. | | | Признаки сравнения. |