Числовые ряды. Сумма ряда.

1.1. Пусть дана числовая последовательность

Выражение вида

(36)

называется числовым рядом или просто рядом. При этом 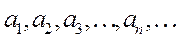называется членами ряда, а член - произвольным номером – общим членом ряда.

1.2. Сумма конечного члена первых членов ряда называется 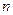-й частичной суммой ряда.

1.3. Если существует конечный предел 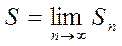, то его называют суммой ряда (36) и ряд называется сходящимся.

1.4. Если 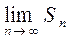не существует, то ряд называется расходящимся.

Например, ряд , (*) составленный из членов геометрической прогрессии с первым членом 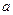и знаменателем .

Сумма 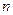первых членов .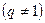

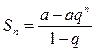Если 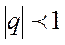, то при 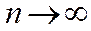, следовательно 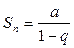, значит ряд (*) сходится.

Если 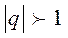, то при , тогда при 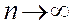, т.е. 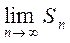не существует. То есть ряд (*) расходится.

Если 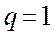, то ряд имеет вид

, , то есть ряд (*) расходится.

Если , то ряд имеет вид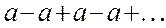

В этом случае

,

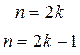
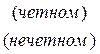т.е. 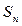предела не имеет - ряд (*) расходится.

Дата добавления: 2015-07-25