Пример 3. Найти общее решение дифференциального уравнения

Найти общее решение дифференциального уравнения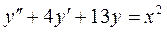

и частное решение, удовлетворяющее начальным условиям 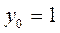, при

Решение.

Характеристическое уравнение имеет вид: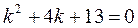

Его корни: (третий вид, )

Тогда

Найдем частное решение по виду правой части (2.3), где

т.е. - многочлен второй степени.

Имеем:

Дифференцируя это равенство два раза и подставляя найденные производные и в исходное уравнение, получаем:

; ;

Раскроем скобки, приведем подобные члены и приравняем коэффициенты в обеих частях равенства при 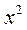, , . В результате получается:

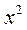13A=1

13B+8A=0

13C+4B+2A=0

Откуда ;

; ;

; ; .

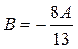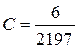И следовательно,

Общее решение исходного уравнения:

Найдем частное решение уравнения, удовлетворяющее начальным условиям: 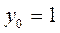, при

Продифференцируем общее решение уравнения, получим:

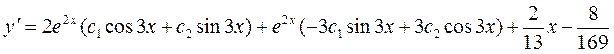Полагая , при , получим систему уравнений:

Решив ее имеем: ,

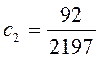
Следовательно, искомое частное решение имеет вид

Задачи 81-90

Для решения задач №81-90 необходимо изучить следующие темы:

1. Числовые ряды. Сумма ряда [2] гл. XVI §1

2. Основные свойства сходящихся числовых рядов [2]гл. XVI §1

3. Необходимый признак сходимости [2] гл. XVI §2

4. Признак сравнения [2] гл. XVI §3

5. Признак Даламбера [2] гл. XVI §4

6. Признак Коши [2] гл. XVI §5

7. Интегральный признак Коши [2] гл. XVI §6

8. Знакочередующиеся ряды. Признак Лейбница [2] гл. XVI §7

9. Функциональные ряды. Область сходимости [2] гл. XVI §8

10. Степенные ряды. Интервал сходимости [2] гл. XVI §13

Указанные разделы учебников содержат следующие основные теоретические сведения

Дата добавления: 2015-07-25