Читайте также:
|
4.1. Первый признак сравнения.
Пусть даны два ряда с положительными членами
(39)
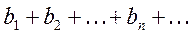(40)
причем каждый член ряда (39) превосходит соответствующего члене ряда (40), т.е. 
(
). Тогда если сходится ряд (40), то и сходится ряд (39); если расходится ряд (39), то и расходится ряд (40).
4.2. Второй признак сравнения.
Если существует конечный и отличный от нуля предел 
, то оба ряда 
и 
одновременно сходятся или одновременно расходятся.
Дата добавления: 2015-07-25; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Необходимый признак сходимости. | | | Интегральный признак сходимости. |