
Читайте также:
|
| Варіант № 1 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:
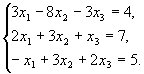
| Варіант №2 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 3 |
1. Обчисліть визначник:
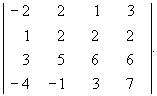
2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 4 |
1. Обчисліть визначник:
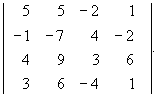
2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 5 |
1. Обчисліть визначник:
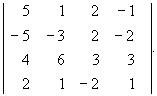
2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:
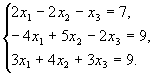
| Варіант № 6 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 7 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 8 |
1. Обчисліть визначник:
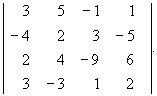
2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 9 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

| Варіант № 10 |
1. Обчисліть визначник:

2. Вирішіть систему за правилом Крамера, методом Гауса і методом оберненої матриці:

Дата добавления: 2015-07-12; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приклад. | | | Завдання до 2 модулю |