Приклад. Обчислимо інтеграл , застосувавши формулу інтегрування по частинах двічі підряд

Обчислимо інтеграл 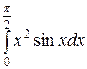, застосувавши формулу інтегрування по частинах двічі підряд. Маємо:

.

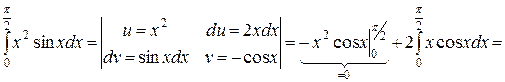
Тема 14. Диференціальні рівняння першого порядку.

Диференціальним рівнянням називається рівняння, що зв'язує незалежні змінні, їх функцію й похідні (або диференціали) цієї функції. Символічно диференціальне рівняння записується у вигляді:

Якщо незалежна змінна одна, то рівняння називається звичайним; якщо ж незалежних змінних дві або більше, те рівняння називається диференціальним рівнянням у частинних похідних.

Найвищий порядок похідної, що входить у рівняння, називається порядком диференціального рівняння.

Рішенням диференціального рівняння називається така диференцируєма функція y =φ(х), яка при підстановці в рівняння замість невідомої функції обертає його в тотожність.

Загальним рішенням диференціального рівняння першого порядку у'=f(х,у) в області D називається функція y = φ (х, С), щомає наступні властивості:

1) вона є рішенням даного рівняння при будь-яких значеннях довільної постійної С, що належать деякій множині;

2) для будь-якої початкової умови y (х_о)=Уо такого, що (х₀; у₀)ЄD, існує єдине значення С= С_о, при якім рішення y = φ (х, С₀) задовольняє заданій початковій умові.

Усяке рішення y = φ(х, С₀), щовиходить із загального рішення y = φ(х, С) при конкретному значенні С =С₀, називається частинним рішенням.

Задача, у якій потрібно знайти приватне рішення рівняння у'= f (х,у), щозадовольняє початковій умові y (х_а)= y ₀, називається задачею Коші.

Процес знаходження рішень диференціального рівняння називається інтегруванням диференціального рівняння.

Найпростіше диференціальне рівняння – це рівняння виду:

Інтегруючи n раз обидві частини рівняння, знайдемо загальне рішення, що залежить від n констант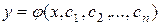

Приклад: Знайти частиннее рішення рівняння з початковими даними: при x=0 y=1, 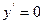. Інтегруємо двічі маємо:

,

З початкових умов випливає: Таким чином, - шукане рішення диференціального рівняння.

Диференціальне рівняння

(14.1)

називається рівнянням з змінними, що розділяються.

Множачи обидві частини рівняння на , одержуємо рівняння з розділеними змінними

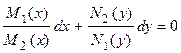(14.2)

У рівнянні (14.2) коефіцієнт при dx залежить тільки від x, а коефіцієнт при dy залежить тільки від y. Виходить, у рівнянні (14.2) змінні розділені. Інтегруючи, одержуємо:

Дата добавления: 2015-07-12